
【题目】如图,等边![]() 外有一点
外有一点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.


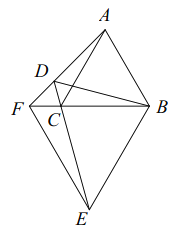
图1 图2 图3
(1)如图1,若![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
(2)如图2,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,以
,以![]() 为边向下作等边
为边向下作等边![]() ,若点
,若点![]() ,
,![]() ,
,![]() 在同一直线上,且
在同一直线上,且![]() ,直接写出
,直接写出![]() 的度数为___________(结果用含
的度数为___________(结果用含![]() 的式子表示).
的式子表示).
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,证明
,证明![]() ,即可证明;
,即可证明;
(2)在![]() 上取点
上取点![]() ,使
,使![]() ,得到
,得到![]() 为等边三角形,再证明
为等边三角形,再证明![]() ,得到
,得到![]() ,即可证明;
,即可证明;
(3)先根据等边三角形的性质证明△ABF≌CBE,得到∠1=∠2,再得到![]() ,由(1)得
,由(1)得![]() ,再得到F,E,B,D四点共圆,得到∠3=∠DBF即可求解.
,再得到F,E,B,D四点共圆,得到∠3=∠DBF即可求解.
(1)过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,

∵![]()
又![]()
∴![]()
又BC=BA
∴![]() (AAS)
(AAS)
![]() ,
,
![]() 平分
平分![]() ;
;
(2)在![]() 上取点
上取点![]() ,使
,使![]() ,
,
∵![]()
![]()
![]() 为等边三角形,
为等边三角形,
∴∠DCE=∠ACB=60°,
∵∠DCE-∠ACE =∠ACB-∠ACE
∴∠DCA=∠ECB
又DC=EC,AC=BC
∴![]() ,
,
![]() ,
,
∴BD-CD=BD-DE=BE=AD
![]() ;
;

(3)如图,∵△ABC,△BEF为等边三角形,
∴AB=CB,BF=BE,∠ABF=∠CBE
∴△ABF≌CBE,
∴∠1=∠2,
∵∠2+∠3=60°,∠4=60°
∴∠FDE=180°-∠1-∠4-∠3=60°
∴∠ADC=120°,
∴![]() ,
,
由(1)得![]() 平分
平分![]()
∴![]() ,
,
∴∠FDB=120°,
∴∠FDB+∠FEB=180°,
∴F,E,B,D四点共圆,
∴∠3=∠DBF
∵∠DBF=60°-![]()
∴∠3=![]() .
.
故答案为![]() .
.



科目:初中数学 来源: 题型:
【题目】某商人经营甲、乙两种商品,每件甲种商品的利润率为![]() ,每件乙种商品的利润率为
,每件乙种商品的利润率为![]() ,当售出的乙种商品的件数比甲种商品的件数多
,当售出的乙种商品的件数比甲种商品的件数多![]() 时,这个商人得到的总利润率是
时,这个商人得到的总利润率是![]() ;当售出的乙种商品的件数比甲种商品的件数少
;当售出的乙种商品的件数比甲种商品的件数少![]() 时,这个商人得到的总利润率是__________. (注:利润率
时,这个商人得到的总利润率是__________. (注:利润率![]() ,总利润率
,总利润率![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一分钟投篮测试规定:满分为![]() 分,成绩达到
分,成绩达到![]() 分及以上为合格,成绩达到
分及以上为合格,成绩达到![]() 分及以上为优秀.甲、乙两组各
分及以上为优秀.甲、乙两组各![]() 名学生的某次测试成绩如下:
名学生的某次测试成绩如下:
成绩(分) |
|
|
|
|
|
|
|
|
|
|
甲组(人) |
|
|
|
|
|
|
|
|
|
|
乙组(人) |
|
|
|
|
|
|
|
|
|
|
![]() 请补充完成下面的成绩分析表:
请补充完成下面的成绩分析表:
统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
甲组 |
|
|
|
| ________ |
乙组 | ________ |
| ________ |
|
|
![]() 你认为甲、乙两组哪一组的投篮成绩较好?请写出两条支持你的观点的理由.
你认为甲、乙两组哪一组的投篮成绩较好?请写出两条支持你的观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() (
(![]() ,
,![]() 是常数,
是常数,![]() )的图象过
)的图象过![]() ,
,![]() 两点.
两点.
(1)在图中画出该一次函数并求其表达式;

(2)若点![]() 在该一次函数图象上,求
在该一次函数图象上,求![]() 的值;
的值;
(3)把![]() 的图象向下平移3个单位后得到新的一次函数图象,在图中画出新函数图形,并直接写出新函数图象对应的表达式.
的图象向下平移3个单位后得到新的一次函数图象,在图中画出新函数图形,并直接写出新函数图象对应的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读新知:化简后,一般形式为ax4+bx2+c=0(a≠0)的方程,由于其具有只含有未知数偶次项的四次方程,我们称其为“双二次方程”.这类方程我们一般可以通过换元法求解.如:求解2x4-5x2+3=0的解.
解:设![]() ,则原方程可化为:
,则原方程可化为:![]() ,解之得
,解之得![]()
当![]() 时,
时,![]() , ∴
, ∴![]() ;
;
当![]() 时
时 ![]() ∴
∴![]() .
.
综上,原方程的解为:![]() ,
,![]() .
.
(1)通过上述阅读,请你求出方程![]() 的解;
的解;
(2)判断双二次方程ax4+bx2+c=0(a≠0)根的情况,下列说法正确的是 (选出正确的答案).
①当b2-4ac≥0时,原方程一定有实数根;
②当b2-4ac<0时,原方程一定没有实数根;
③原方程无实数根时,一定有b2-4ac<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
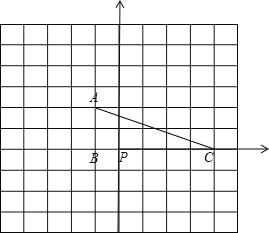
【题目】如图,△ABC中任意一点P(xo,yo),将△ABC平移后得到△A1B1C1,点P的对应点P1(xo+6,yo+4).
(1)写出A1、B1、C1的坐标.
(2)若三角形外有一点M经过同样的平移后得到点N(5,3),写出M点关于原点对称的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑500米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲.乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①100秒时乙到达终点;②a=8;③b=92④c=125,其中正确的是( )

A.②③B.①②③C.②③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com