
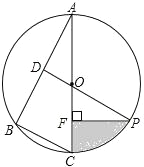
【题目】如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=4,点D是AB的中点,连接DO并延长交⊙O于点P.
(1)求劣弧PC的长(结果保留π);
(2)过点P作PF⊥AC于点F,求阴影部分的面积(结果保留π).
【答案】(1)![]() (2)
(2)![]()
【解析】
试题(1) 根据垂经定理及其推论先求出∠POC=∠AOD=60°,然后再根据条件求出圆的半径为2,利用弧长公式计算即可;(2)利用特殊角求出OF,PF的长,然后根据S阴影=S扇形﹣S△OPF代入数值计算即可.
试题解析:解:(1)∵点D是AB的中点,PD经过圆心,
∴PD⊥AB,
∵∠A=30°,
∴∠POC=∠AOD=60°,OA=2OD,
∵PF⊥AC,
∴∠OPF=30°,
∴OF=![]() OP,
OP,
∵OA=OC,AD=BD,
∴BC=2OD,
∴OA=BC=2,
∴⊙O的半径为2,
∴劣弧PC的长=![]() =
=![]() ;
;
(2)∵OF=![]() OP,
OP,
∴OF=1,
∴PF=![]() ,
,
∴S阴影=S扇形﹣S△OPF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
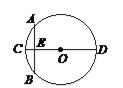
【题目】“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( )
A. ![]() 寸 B. 13寸 C. 25寸 D. 26寸
寸 B. 13寸 C. 25寸 D. 26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
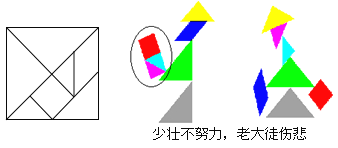
【题目】小明和小儿是同班同学,被分到了同一个学习小组,在一次数学活动课上,他们各自用一张面积为![]() 的正方形纸片制作了一副七巧板,合作完成了如图所示的作品.请计算图中打圈部分的面积是( )
的正方形纸片制作了一副七巧板,合作完成了如图所示的作品.请计算图中打圈部分的面积是( )
少壮不努力,老大徒伤悲
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
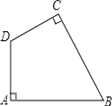
【题目】如图,在四边形ABCD中,∠A=∠C=90°.
(1)用直尺和圆规作⊙O,使它经过A、B、D三点(保留作图痕迹);
(2)点C是否在⊙O上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F ,且DC=FC,点D的坐标为(12,-2).
(1)判断⊙P与x轴的位置关系,并说明理由;
(2)求⊙P半径;
(3)若弧BD上有一动点M,连接AM,过B点作BN⊥AM,垂足为N,连DN,则DN的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
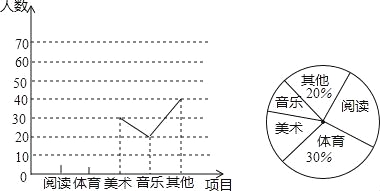
【题目】某学校为了解该校学生的课余活动情况,抽样调查了部分同学,将所得数据处理后,制成折线统计图(部分)和扇形统计图(部分)如下:
(1)在这次研究中,一共调查了 名学生.
(2)补全频数分布折线图;
(3)该校共有2200名学生,估计该校学生中爱好阅读的人数大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:在小学已经学过“正方形的四条边都相等,正方形的四个内角都是直角”,试利用上述知识,并结合已学过的知识解答下列问题:
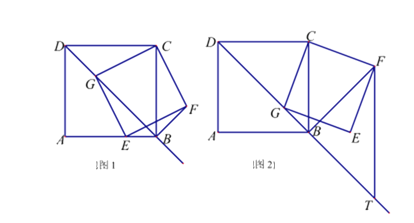
如图1,在正方形ABCD中,G是射线DB上的一个动点(点G不与点D重合),以CG为边向下作正方形CGEF.
(1)当点G在线段BD上时,求证:![]() ;
;
(2)连接BF,试探索:BF,BG与AB的数量关系,并说明理由;
(3)若AB=a(a是常数),如图2,过点F作FT∥BC,交射线DB于点T,问在点G的运动过程中,GT的长度是否会随着G点的移动而变化?若不变,请求出GT的长度;若变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com