【题目】如图，A、B两点在正方形网格的格点上，每个方格都是边长为1的正方形．点C也在格点上，且△ABC为等腰三角形，则符合条件的点C有（ ）个．
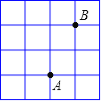
A.3B.5C.8D.10
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】某校为了解学生最喜爱的一项课外活动项目，随机对全校部分学生进行了一次调査，调査结果有三种情况：A．文学艺术；B．科技制作；C．体育运动．并将调查结果绘制成如下的不完整统计图．
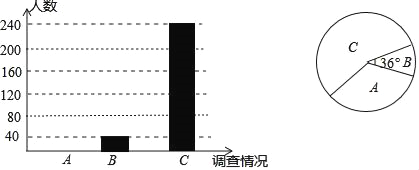
请根据相关信息，解答下列问题：
（1）本次活动共调查了多少名学生？
（2）将条形统计图补充完整，并求出扇形统计图中A所在扇形的圆心角的度数；
（3）若该校共有1400名学生，试估计该校学生中最喜爱文学艺术的人数是多少．
查看答案和解析>>
科目：初中数学 来源： 题型：
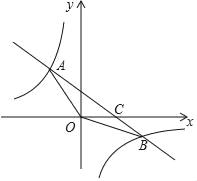
【题目】如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数y=
（m≠0）的图象交于第二、四象限内的A、B两点，与x轴交于点C，点A（﹣2，3），点B（6，n）．
(1)求该反比例函数和一次函数的解析式；
(2)求△AOB的面积；
(3)若M（x1，y1），N（x2，y2）是反比例函数y=（m≠0）的图象上的两点，且x1＜x2，y1＜y2，指出点M、N各位于哪个象限．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题背景：如图
，点
为线段
外一动点，且
，若
，
，连接
，求的最大值．解决方法：以
为边作等边
，连接
，推出
，当点
在
的延长线上时，线段取得最大值
．
问题解决：如图
，点为线段外一动点，且，若，
，连接，当取得最大值时，
的度数为_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，∠B=45°，∠C=30°，点D是BC上一点，连接AD，过点A作AG⊥AD，在AG上取点F，连接DF．延长DA至E，使AE=AF，连接EG，DG，且GE=DF．
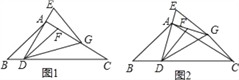
（1）若AB=2
，求BC的长；
（2）如图1，当点G在AC上时，求证：BD=
CG；
（3）如图2，当点G在AC的垂直平分线上时，直接写出
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
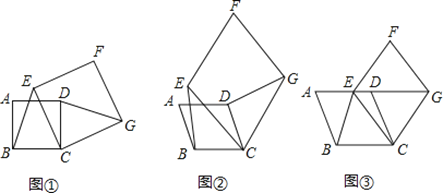
【题目】感知：如图①，四边形ABCD、CEFG均为正方形.易知BE=DG．
探究：如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．
应用：如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD的延长线上.若AE=3ED, ∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
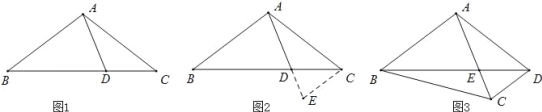
【题目】阅读下面材料：小腾遇到这样一个问题：如图1，在△ABC中，点D在线段BC上，∠BAD=75°，∠CAD=30°，AD=2，BD=2DC，求AC的长．
小腾发现，过点C作CE∥AB，交AD的延长线于点E，通过构造△ACE，经过推理和计算能够使问题得到解决（如图 2）．
请回答：∠ACE的度数为 ，AC的长为 ．
参考小腾思考问题的方法，解决问题：
如图 3，在四边形 ABCD中，∠BAC=90°，∠CAD=30°，∠ADC=75°，AC与BD交于点E，AE=2，BE=2ED，求BC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
