
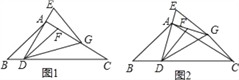
【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
(1)若AB=2![]() ,求BC的长;
,求BC的长;
(2)如图1,当点G在AC上时,求证:BD=![]() CG;
CG;
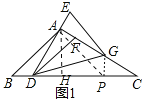
(3)如图2,当点G在AC的垂直平分线上时,直接写出![]() 的值.
的值.
【答案】(1)BC =2+2![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)如图1中,过点A作AH⊥BC于H,分别在RT△ABH,RT△AHC中求出BH、HC即可.
(2)如图1中,过点A作AP⊥AB交BC于P,连接PG,由△ABD≌△APG推出BD=PG,再利用30度角性质即可解决问题.
(3)如图2中,作AH⊥BC于H,AC的垂直平分线交AC于P,交BC于M.则AP=PC,作DK⊥AB于K,设BK=DK=a,则AK=![]() a,AD=2a,只要证明∠BAD=30°即可解决问题.
a,AD=2a,只要证明∠BAD=30°即可解决问题.
试题解析:(1)如图1中,过点A作AH⊥BC于H.
∴∠AHB=∠AHC=90°,
在RT△AHB中,∵AB=2![]()
,∠B=45°,
∴BH=ABcosB=2![]() =2,
=2,
AH=ABsinB=2,
在RT△AHC中,∵∠C=30°,
∴AC=2AH=4,CH=ACcosC=2![]() ,
,
∴BC=BH+CH=2+2![]() .
.
(2)证明:如图1中,过点A作AP⊥AB交BC于P,连接PG,
∵AG⊥AD,∴∠DAF=∠EAC=90°,
在△DAF和△GAE中,
![]()
∴△DAF≌△GAE,
∴AD=AG,
∴∠BAP=90°=∠DAG,
∴∠BAD=∠PAG,
∵∠B=∠APB=45°,
∴AB=AP,
在△ABD和△APG中,
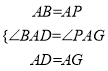
∴△ABD≌△APG,
∴BD=PG,∠B=∠APG=45°,
∴∠GPB=∠GPC=90°,
∵∠C=30°,
∴PG=![]() GC,
GC,
∴BD=![]() CG.
CG.
(3)如图2中,作AH⊥BC于H,AC的垂直平分线交AC于P,交BC于M.则AP=PC,
在RT△AHC中,∵∠ACH=30°,
∴AC=2AH,
∴AH=AP,
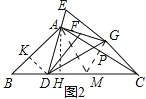
在RT△AHD和RT△APG中,
![]()
∴△AHD≌△APG,
∴∠DAH=∠GAP,
∵GM⊥AC,PA=PC,
∴MA=MC,
∴∠MAC=∠MCA=∠MAH=30°,
∴∠DAM=∠GAM=45°,
∴∠DAH=∠GAP=15°,
∴∠BAD=∠BAH﹣∠DAH=30°,
作DK⊥AB于K,设BK=DK=a,则AK=![]() a,AD=2a,
a,AD=2a,
∴![]()
∵AG=CG=AD,
∴![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
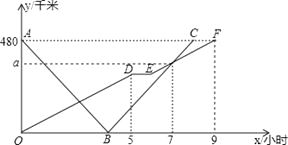
【题目】(本题满分12分)快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数图象如图,请结合图象信息解答下列问题:
(小时)之间的函数图象如图,请结合图象信息解答下列问题:
(1)求慢车的行驶速度和![]() 的值;
的值;
(2)求快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)求两车出发后几小时相距的路程为![]() 千米?
千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中
①两点之间,直线最短;
②经过直线外一点,能作一条直线与这条直线平行;
③和已知直线垂直的直线有且只有一条;
④在平面内过一点有且只有一条直线垂直于已知直线.
正确的是__________.(只需填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资量
与投资量![]() 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润![]() 与投资量
与投资量![]() 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)

(1)分别求出利润![]() 与
与![]() 关于投资量
关于投资量![]() 的函数关系式;
的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
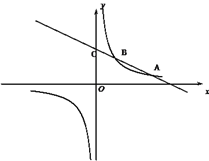
【题目】如图,一次函数![]() (k<0)与反比例函数
(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1),B(n,2))
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1),B(n,2))
(1)求反比例函数和一次函数的解析式;
(2)写出![]() >
>![]() 时,
时, ![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com