
【题目】如图所示,直线AB、CD相交于点O。若OM=ON=MN,那么∠APQ+∠CQP=。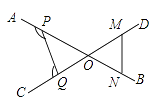
【答案】240
【解析】解 :∵OM=ON=MN,
∴△OMN是一个等边三角形,
∴∠MON=60° ,
∴∠POQ=∠MON=60° ,
∵∠APQ=∠POQ+∠PQO=60°+∠PQO, ∠PQC=∠QPO+∠POQ=∠QPO+60°,
∴∠APQ+∠CQP=∠POQ+∠PQO+∠QPO+∠POQ=60°+∠PQO+∠QPO+∠POQ;
∵∠PQO+∠QPO+∠POQ=180° ;
∴∠APQ+∠CQP=60°+∠PQO+∠QPO+∠POQ=60°+180°=240°.
【考点精析】根据题目的已知条件,利用三角形的内角和外角和三角形的外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A.0既不是正数,也不是负数
B.若仓库运进货物5t记作+5t,那么运出货物5t记作﹣5t
C.0是自然数,也是整数,也是有理数
D.一个有理数不是正数,那它一定是负数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
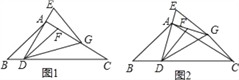
(1)若AB=2![]() ,求BC的长;
,求BC的长;
(2)如图1,当点G在AC上时,求证:BD=![]() CG;
CG;
(3)如图2,当点G在AC的垂直平分线上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁都县某脐橙园2016年产量为1000吨,2018年产量为1440吨,求该脐橙园脐橙产量的年平均增长率,设该脐橙园脐橙产量的年平均增长量为x,则根据题意可列方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点A(﹣1,y1)、B(1,y2)、C(2,y3)是抛物线y=﹣2(x﹣1)2+m上的三点,则y1、y2,y3的大小关系的是_____(用“<”连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】In right Fig.,if the length of the segment AB is 1,M is the midpoint of the segment AB,and point C divides the segment MB into two parts such that MC:CB=1:2,then the length of AC is 。
(英汉词典:length 长度;segment 线段;midpoint 中点;divides…into 分为,分成)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ. 
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
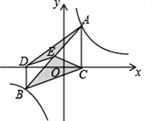
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com