
【题目】列方程解应用题:第19届亚洲运动会将于2022年9月10日至25日在杭州举行,杭州奥体博览城将成为杭州2022年亚运会的主场馆,某工厂承包了主场馆建设中某一零件的生产任务,需要在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多![]() ,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
【答案】(1)原计划每天生产的零件2400个,规定的天数是10天;(2)原计划安排的工人人数480人.
【解析】
(1)根据题意可设原计划每天生产的零件x个,根据时间是一定的,列出方程求得原计划每天生产的零件个数,再根据工作时间=工作总量÷工作效率,即可求得规定的天数;
(2)设原计划安排的工人人数为y人,根据等量关系:恰好提前两天完成2400个零件的生产任务,列出方程求解即可.
(1)解:设原计划每天生产的零件x个,由题意得,
![]()
得:x=2400经检验,x=2400是原方程的根,且符合题意.∴规定的天数为24000÷2400=10(天).
答:原计划每天生产的零件2400个,规定的天数是10天;
(2)设原计划安排的工人人数为y人,依题意有
[5×20×(1+20%)×![]() +2400]×(10﹣2)=24000,解得y=480,
+2400]×(10﹣2)=24000,解得y=480,
经检验,y=480是原方程的根,且符合题意.答:原计划安排的工人人数480人.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边![]() 中,点
中,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 的延长线上,
的延长线上,![]() (如图1)
(如图1)
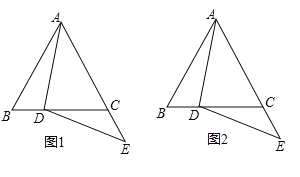
(1)求证:![]() ;
;
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,
,![]() .
.
①依题意将图2补全;
②证明:在点![]() 运动的过程中,始终有
运动的过程中,始终有![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
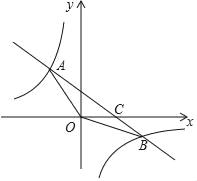
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A(﹣2,3),点B(6,n).
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A(﹣2,3),点B(6,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y=![]() (m≠0)的图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限.
(m≠0)的图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的最大值.解决方法:以
的最大值.解决方法:以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,推出
,推出![]() ,当点
,当点![]() 在
在![]() 的延长线上时,线段
的延长线上时,线段![]() 取得最大值
取得最大值![]() .
.
问题解决:如图![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,若
,若![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() 取得最大值时,
取得最大值时,![]() 的度数为_________.
的度数为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
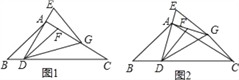
(1)若AB=2![]() ,求BC的长;
,求BC的长;
(2)如图1,当点G在AC上时,求证:BD=![]() CG;
CG;
(3)如图2,当点G在AC的垂直平分线上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
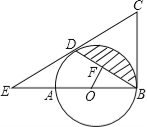
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com