
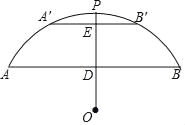
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米,
(1)求圆弧所在的圆的半径r的长;
(2)若拱顶离水面只有4米,即PE=4米时,求它的跨度A′B′.
科目:初中数学 来源: 题型:
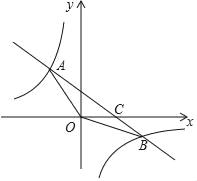
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A(﹣2,3),点B(6,n).
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点A(﹣2,3),点B(6,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y=![]() (m≠0)的图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限.
(m≠0)的图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限.
查看答案和解析>>
科目:初中数学 来源: 题型:
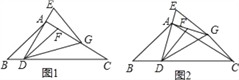
【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
(1)若AB=2![]() ,求BC的长;
,求BC的长;
(2)如图1,当点G在AC上时,求证:BD=![]() CG;
CG;
(3)如图2,当点G在AC的垂直平分线上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
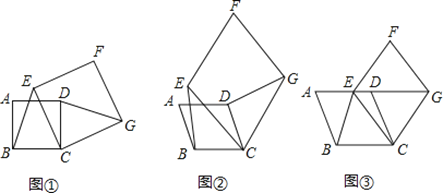
【题目】感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.
探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
应用:如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED, ∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班从学校出发去某景点旅游,全班分成甲、乙两组,甲组乘坐大型客车,乙组乘坐小型客车.已知甲组比乙组先出发,汽车行驶的路程![]() (单位:
(单位:![]() )和行驶时间
)和行驶时间![]() (单位:
(单位:![]() )之间的函数关系如图所示.
)之间的函数关系如图所示.
根据图象信息,回答下列问题:
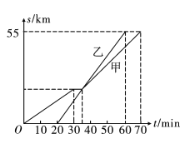
(1)学校到景点的路程为_ ,甲组比乙组先出发 , 组先到达旅游景点;
(2)求乙组乘坐的小型客车的平均速度;
(3)从图象中你还能获得哪些信息? (请写出一条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
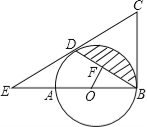
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
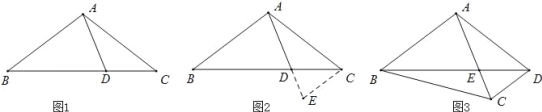
【题目】阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:∠ACE的度数为 ,AC的长为 .
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
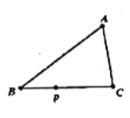
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以2
以2![]() 的速度运动,设运动时间为
的速度运动,设运动时间为![]()
![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或12或4C.
或12或4C.![]() 或
或![]() 或12D.
或12D.![]() 或12或4
或12或4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com