
ΓΨΧβΡΩΓΩΓΑ–Θ‘ΑΑ≤»ΪΓ± ήΒΫ»Ϊ…γΜαΒΡΙψΖΚΙΊΉΔΘ§Ρ≥÷–―ßΕ‘≤ΩΖ÷―ß…ζΨΆ–Θ‘ΑΑ≤»Ϊ÷Σ ΕΒΡΝΥΫβ≥ΧΕ»Θ§≤…”ΟΥφΜζ≥ι―υΒς≤ιΒΡΖΫ ΫΘ§≤ΔΗυΨί ’Φ·ΒΫΒΡ–≈œΔΫχ––Ά≥ΦΤΘ§Μφ÷ΤΝΥœ¬ΟφΝΫΖυ…–≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΗυΨίΆ≥ΦΤΆΦ÷–ΥυΧαΙ©ΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
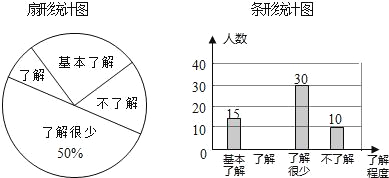
Θ®1Θ©Ϋ” ήΈ ΨμΒς≤ιΒΡ―ß…ζΙ≤”–ΓΓ ΓΓ»ΥΘ§…»–ΈΆ≥ΦΤΆΦ÷–ΓΑΜυ±ΨΝΥΫβΓ±≤ΩΖ÷ΥυΕ‘”Π…»–ΈΒΡ‘≤–ΡΫ«ΈΣΓΓ ΓΓΕ»ΘΜ
Θ®2Θ©«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®3Θ©»τΗΟ÷–―ßΙ≤”–―ß…ζ900»ΥΘ§«κΗυΨί…œ ωΒς≤ιΫαΙϊΘ§ΙάΦΤΗΟ÷–―ß―ß…ζ÷–Ε‘–Θ‘ΑΑ≤»Ϊ÷Σ Ε¥οΒΫΓΑΝΥΫβΓ±ΚΆΓΑΜυ±ΨΝΥΫβΓ±≥ΧΕ»ΒΡΉή»Υ ΐΘ°
ΓΨ¥πΑΗΓΩ(1) 60Θ§90ΘΜ(2)ΦϊΫβΈω;(3) 300»Υ
ΓΨΫβΈωΓΩ
Θ®1Θ©”…ΝΥΫβΚή…ΌΒΡ”–30»ΥΘ§’Φ50%Θ§Ω…«σΒΟΫ” ήΈ ΨμΒς≤ιΒΡ―ß…ζ ΐΘ§ΦΧΕχ«σΒΟ…»–ΈΆ≥ΦΤΆΦ÷–ΓΑΜυ±ΨΝΥΫβΓ±≤ΩΖ÷ΥυΕ‘”Π…»–ΈΒΡ‘≤–ΡΫ«ΘΜ
Θ®2Θ©”…Θ®1Θ©Ω…«σΒΟΝΥΫβΒΡ»Υ ΐΘ§ΦΧΕχ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®3Θ©άϊ”Ο―υ±ΨΙάΦΤΉήΧεΒΡΖΫΖ®Θ§Φ¥Ω…«σΒΟ¥πΑΗΘ°
ΫβΘΚΘ®1Θ©ΓΏΝΥΫβΚή…ΌΒΡ”–30»ΥΘ§’Φ50%Θ§
ΓύΫ” ήΈ ΨμΒς≤ιΒΡ―ß…ζΙ≤”–ΘΚ30Γ¬50%=60Θ®»ΥΘ©ΘΜ
Γύ…»–ΈΆ≥ΦΤΆΦ÷–ΓΑΜυ±ΨΝΥΫβΓ±≤ΩΖ÷ΥυΕ‘”Π…»–ΈΒΡ‘≤–ΡΫ«ΈΣΘΚ![]() ΓΝ360Γψ=90ΓψΘΜ
ΓΝ360Γψ=90ΓψΘΜ
Ι ¥πΑΗΈΣΘΚ60Θ§90ΘΜ
Θ®2Θ©60©¹15©¹30©¹10=5ΘΜ
≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΒΟΘΚ
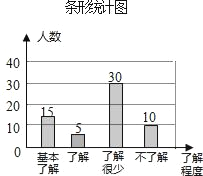
Θ®3Θ©ΗυΨίΧβ“βΒΟΘΚ900ΓΝ![]() =300Θ®»ΥΘ©Θ§
=300Θ®»ΥΘ©Θ§
‘ρΙάΦΤΗΟ÷–―ß―ß…ζ÷–Ε‘–Θ‘ΑΑ≤»Ϊ÷Σ Ε¥οΒΫΓΑΝΥΫβΓ±ΚΆΓΑΜυ±ΨΝΥΫβΓ±≥ΧΕ»ΒΡΉή»Υ ΐΈΣ300»ΥΘ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐy=ax2+bx+c+2ΒΡΆΦœσ»γΆΦΥυ ΨΘ§ΕΞΒψΈΣΘ®©¹1Θ§0Θ©Θ§œ¬Ν–Ϋα¬έΘΚΔΌabcΘΦ0ΘΜΔΎb2©¹4ac=0ΘΜΔέaΘΨ2ΘΜΔή4a©¹2b+cΘΨ0Θ°Τδ÷–’ΐ»ΖΫα¬έΒΡΗω ΐ «Θ® Θ©
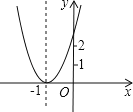
AΘ°1 BΘ°2 CΘ°3 DΘ°4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ÷±œΏ![]() ΒΡΫβΈω Ϋ «
ΒΡΫβΈω Ϋ «![]() Θ§≤Δ«“”κ
Θ§≤Δ«“”κ![]() ÷αΓΔ
÷αΓΔ![]() ÷αΖ÷±πΫΜ”ΎAΓΔBΝΫΒψΘ°“ΜΗωΑκΨΕΈΣ1.5ΒΡΓ―CΘ§‘≤–ΡC¥”ΒψΘ®0Θ§1.5Θ©ΩΣ Φ“‘ΟΩΟκ0.5ΗωΒΞΈΜΒΡΥΌΕ»―ΊΉ≈
÷αΖ÷±πΫΜ”ΎAΓΔBΝΫΒψΘ°“ΜΗωΑκΨΕΈΣ1.5ΒΡΓ―CΘ§‘≤–ΡC¥”ΒψΘ®0Θ§1.5Θ©ΩΣ Φ“‘ΟΩΟκ0.5ΗωΒΞΈΜΒΡΥΌΕ»―ΊΉ≈![]() ÷αœρœ¬‘ΥΕ·Θ§Β±Γ―C”κ÷±œΏ
÷αœρœ¬‘ΥΕ·Θ§Β±Γ―C”κ÷±œΏ![]() œύ«– ±Θ§‘ρΗΟ‘≤‘ΥΕ·ΒΡ ±ΦδΈΣΘ®ΓΓΓΓΘ©
œύ«– ±Θ§‘ρΗΟ‘≤‘ΥΕ·ΒΡ ±ΦδΈΣΘ®ΓΓΓΓΘ©
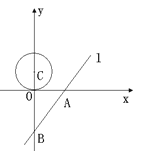
A. 3ΟκΜρ6Οκ B. 6Οκ C. 3Οκ D. 6ΟκΜρ16Οκ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–Έ÷ΫΤ§![]() ÷–Θ§
÷–Θ§![]() Θ§Βψ
Θ§Βψ![]() Ζ÷±π‘Ύ
Ζ÷±π‘Ύ![]() …œΘ§Α―
…œΘ§Α―![]() ―Ί
―Ί![]() Ζ≠’έΘ§
Ζ≠’έΘ§![]() ΒΡ¬δΒψ «Ε‘Ϋ«œΏ
ΒΡ¬δΒψ «Ε‘Ϋ«œΏ![]() …œΒΡΒψ
…œΒΡΒψ![]() ΚΆ
ΚΆ![]() Θ§‘ρΥΡ±Ώ–Έ
Θ§‘ρΥΡ±Ώ–Έ![]() ΒΡΟφΜΐ «____________Θ°
ΒΡΟφΜΐ «____________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒ»±ΏΓςABCΒΡΝΫΗωΕΞΒψΉχ±ξΈΣAΘ®-3Θ§0Θ©Θ§BΘ®3Θ§0Θ©Θ§‘ρΒψ![]() ΒΡΉχ±ξΈΣ____Θ§ΓςABCΒΡΟφΜΐΈΣ____Θ°
ΒΡΉχ±ξΈΣ____Θ§ΓςABCΒΡΟφΜΐΈΣ____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
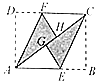
ΓΨΧβΡΩΓΩΝΫΗω»ΪΒ»ΒΡ÷±Ϋ«»ΐΫ«–ΈABCΚΆDEF÷ΊΒΰ‘Ύ“ΜΤπΘ§Τδ÷–ΓœACB=ΓœDFE=90ΓψΘ§ΓœA=ΓœFDE=60ΓψΘ§AC=1. ΙΧΕ®ΓςABC≤ΜΕ·Θ§ΫΪΓςDEFΫχ––»γœ¬≤ΌΉςΘΚ
(1) »γΆΦ (1)Θ§ΓςDEF―ΊœΏΕΈABœρ”“ΤΫ“Τ(Φ¥DΒψ‘ΎœΏΕΈABΡΎ“ΤΕ·)Θ§Ν§ΫαDCΓΔCFΓΔFBΘ§ΥΡ±Ώ–ΈCDBFΒΡ–ΈΉ¥‘Ύ≤ΜΕœΒΡ±δΜ·Θ§ΒΪΥϋΒΡΟφΜΐ≤Μ±δΜ·Θ§«κ«σ≥ωΤδΟφΜΐ.
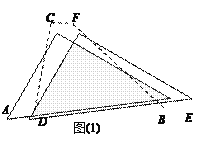
(2)»γΆΦ(2)Θ§Β±DΒψ“ΤΒΫABΒΡ÷–Βψ ±Θ§«κΡψ≤¬œκΥΡ±Ώ–ΈCDBFΒΡ–ΈΉ¥Θ§≤ΔΥΒΟςάμ”….

(3)»γΆΦ(3)Θ§ΓςDEFΒΡFΒψΙΧΕ®‘ΎABΒΡ÷–ΒψΘ§»ΜΚσ»ΤFΒψΑ¥Υ≥ ±’κΖΫœρ–ΐΉΣΓςDEFΘ§ ΙEFΫΜ‘ΎAC±Ώ…œ”ΎMΘ§FDΫΜBC”ΎNΘ§»τFM=x,FN=y, ‘«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΓΘ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψAΘ§BΒΡΉχ±ξΖ÷±πΈΣAΘ®Θ≠1Θ§0Θ©Θ§BΘ®3Θ§0Θ©Θ§œ÷Ά§ ±ΫΪΒψAΘ§BΖ÷±πœρ…œΤΫ“Τ2ΗωΒΞΈΜΘ§‘Όœρ”“ΤΫ“Τ1ΗωΒΞΈΜΘ§Ζ÷±πΒΟΒΫΒψAΘ§BΒΡΕ‘”ΠΒψCΘ§DΘ§Ν§Ϋ”ACΘ§BDΘ§CDΘ°
Θ®1Θ©«σΒψCΘ§DΒΡΉχ±ξΦΑΥΡ±Ώ–ΈABDCΒΡΟφΜΐSΥΡ±Ώ–ΈABDCΘ°(Χα ΨΘΚΤΫ––ΥΡ±Ώ–ΈΒΡΟφΜΐ=ΒΉΓΝΗΏ)
Θ®2Θ©‘Ύy÷α…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§Ν§Ϋ”PAΘ§PBΘ§ ΙSΓςPAB=SΥΡ±Ώ–ΈABDCΘΩ»τ¥φ‘Ύ’β―υ“ΜΒψΘ§«σ≥ωΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§ ‘ΥΒΟςάμ”…Θ°
Θ®3Θ©ΒψP «œΏΕΈBD…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”PCΘ§POΘ§Β±ΒψP‘ΎBD…œ“ΤΕ· ±Θ®≤Μ”κBΘ§D÷ΊΚœΘ©![]() ΒΡ÷Β «ΖώΖΔ…ζ±δΜ·Θ§»τ≤Μ±δ«κ«σ≥ωΗΟ÷ΒΘ§»τΜα±δ«κ≤Δ«κΥΒΟςάμ”…Θ°
ΒΡ÷Β «ΖώΖΔ…ζ±δΜ·Θ§»τ≤Μ±δ«κ«σ≥ωΗΟ÷ΒΘ§»τΜα±δ«κ≤Δ«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“Ο«‘ΦΕ®Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Ψ≠ΙΐœσœόΡΎΡ≥Βψ«“ΤΫ––”ΎΉχ±ξ÷αΜρΤΫ––”ΎΝΫΉχ±ξ÷αΦ–Ϋ«ΤΫΖ÷œΏΒΡ÷±œΏΘ§Ϋ–ΗΟΒψΒΡΓΑ≤Έ’’œΏΓ±Θ°άΐ»γΘ§Βψ
÷–Θ§Ψ≠ΙΐœσœόΡΎΡ≥Βψ«“ΤΫ––”ΎΉχ±ξ÷αΜρΤΫ––”ΎΝΫΉχ±ξ÷αΦ–Ϋ«ΤΫΖ÷œΏΒΡ÷±œΏΘ§Ϋ–ΗΟΒψΒΡΓΑ≤Έ’’œΏΓ±Θ°άΐ»γΘ§Βψ![]() ΒΡ≤Έ’’œΏ”–ΘΚ
ΒΡ≤Έ’’œΏ”–ΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ®»γΆΦ1Θ©Θ°
Θ®»γΆΦ1Θ©Θ°
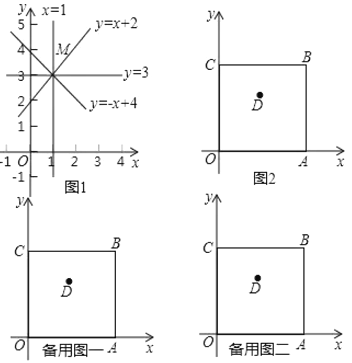
»γΆΦ2Θ§’ΐΖΫ–Έ![]() ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ
‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ‘ΎΒΎ“ΜœσœόΘ§Βψ
‘ΎΒΎ“ΜœσœόΘ§Βψ![]() Θ§
Θ§![]() Ζ÷±π‘Ύ
Ζ÷±π‘Ύ![]() ÷αΚΆ
÷αΚΆ![]() ÷α…œΘ§Βψ
÷α…œΘ§Βψ![]() ‘Ύ’ΐΖΫ–ΈΡΎ≤ΩΘ°
‘Ύ’ΐΖΫ–ΈΡΎ≤ΩΘ°
Θ®1Θ©÷±Ϋ”–¥≥ωΒψ![]() ΒΡΥυ”–≤Έ’’œΏΘΚ ΘΜ
ΒΡΥυ”–≤Έ’’œΏΘΚ ΘΜ
Θ®2Θ©»τ![]() Θ§Βψ
Θ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§«“Βψ
ΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§«“Βψ![]() ”–“ΜΧθ≤Έ’’œΏ «
”–“ΜΧθ≤Έ’’œΏ «![]() Θ§‘ρΒψ
Θ§‘ρΒψ![]() ΒΡΉχ±ξ «_______________ΘΜ
ΒΡΉχ±ξ «_______________ΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Βψ![]() «
«![]() ±Ώ…œ»Έ“β“ΜΒψΘ®Βψ
±Ώ…œ»Έ“β“ΜΒψΘ®Βψ![]() ≤Μ”κΒψ
≤Μ”κΒψ![]() Θ§
Θ§![]() ÷ΊΚœΘ©Θ§Ν§Ϋ”
÷ΊΚœΘ©Θ§Ν§Ϋ”![]() Θ§ΫΪ
Θ§ΫΪ![]() ―ΊΉ≈
―ΊΉ≈![]() ’έΒΰΘ§Βψ
’έΒΰΘ§Βψ![]() ΒΡΕ‘”ΠΒψΦ«ΈΣ
ΒΡΕ‘”ΠΒψΦ«ΈΣ![]() Θ°Β±Βψ
Θ°Β±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ΒΡΤΫ––”ΎΉχ±ξ÷αΒΡ≤Έ’’œΏ…œ ±Θ§–¥≥ωœύ”ΠΒΡ’έΚέ
ΒΡΤΫ––”ΎΉχ±ξ÷αΒΡ≤Έ’’œΏ…œ ±Θ§–¥≥ωœύ”ΠΒΡ’έΚέ![]() Υυ‘Ύ÷±œΏΒΡΫβΈω ΫΘΚ Θ°
Υυ‘Ύ÷±œΏΒΡΫβΈω ΫΘΚ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡ±Ώ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() «
«![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ°
Θ°

Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–Έ![]() «Νβ–ΈΘ°
«Νβ–ΈΘ°
Θ®2Θ©»τ![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com