
分析 (1)观察题目隐含的数字规律可直接写出.
(2)直接利用规律(1),将相邻两个正整数的积的倒数化成它们的倒数的差进行计算即可.
(3)每一项提出$\frac{1}{4}$,可将$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2012×2014}$化成$\frac{1}{4}$×($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{1006}$-$\frac{1}{1007}$),然后直接应用规律进行简化运算即可.
解答 解:(1)答案为:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$
=1-$\frac{1}{2015}$
=$\frac{2014}{2015}$
(3)$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2012×2014}$
=$\frac{1}{4}$×($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{1006}$-$\frac{1}{1007}$)
=$\frac{1}{4}$×$\frac{1006}{1007}$
=$\frac{503}{2014}$
点评 本题考查了数字的变化规律问题,解题的关键是能够总结出题目隐含的数字规律并加以运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
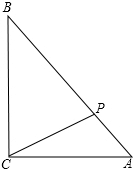 如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.
如图所示,在R△ABC中,∠C=90°,AC=6,AB=10,点P为AB上一点,设PB=x,△ACP的面积为y,写出y与x之间的函数关系式及x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.97×107 | B. | 6.0×107 | C. | 5.97×108 | D. | 6.0×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com