
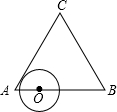
 如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第4秒.
如图,动点O从边长为6的等边△ABC的顶点A出发,沿着A→C→B→A的路线匀速运动一周,速度为1个单位长度每秒.以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第4秒. 分析 若以O为圆心,以$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第二次相切,即为当点O在AC上,且和BC边相切的情况.作O′D⊥BC于D,则O′D=$\sqrt{3}$,利用解直角三角形的知识,进一步求得O′C=2,从而求得OA的长,进一步求得运动时间.
解答 解:根据题意,则作O′D⊥BC于D,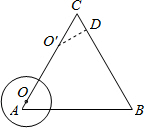
则O′D=$\sqrt{3}$,
在直角三角形O′CD中,∠C=60°,O′D=$\sqrt{3}$,
∴O′C=2,
∴O′A=6-2=4,
∴以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第4秒.
故答案为:4.
点评 本题考查了直线和圆相切时数量之间的关系的应用,能够正确分析出以O为圆心、$\sqrt{3}$为半径的圆在运动过程中与△ABC的边第二次相切时的位置是解此题的关键,此题是一道中档题目,难度适中.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{90}{x+2}$=$\frac{70}{x}$ | B. | $\frac{90}{x-2}$=$\frac{70}{x}$ | C. | $\frac{90}{x}$=$\frac{70}{x+2}$ | D. | $\frac{90}{x}$=$\frac{70}{x-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
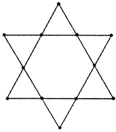 某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你依照举例再设计两种不同的栽树方案(不写作法)
某住宅小区拟栽种12棵风景树,若想栽成6行,每行4棵,且6行树所处位置连成线后能组成精美的对称图案,请你依照举例再设计两种不同的栽树方案(不写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com