练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
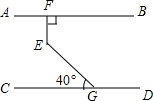
    14．如图，AB∥CD，EF⊥AB于F，∠EGC=40°，则∠FEG=（　　）
    A．120°B．130°C．140°D．150°

    分析 过点E作EH∥AB，再由平行线的性质即可得出结论．

    解答 解：过点E作EH∥AB，
    ∵EH⊥AB于F，
    ∴∠FEH=∠BFE=90°．
    ∵AB∥CD，∠EGC=40°，
    ∴EH∥CD．
    ∴∠HEG=∠EGC=40°，
    ∴∠FEG=∠FEH+∠HEG=90°+40°=130°．
    故选B．

    点评 本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

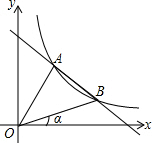    4．如图，直线y=kx+b（k≠0），与反比例函数y=$\frac{m}{x}$（m≠0）的图象交于第一象限内的A、B两点，已知点A的坐标为（3，4），OB与x轴正半轴的夹角为α，且tanα=$\frac{1}{3}$．
    （1）求点B的坐标．
    （2）直接写出使不等式kx+b-$\frac{m}{x}$＞0成立的正整数x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

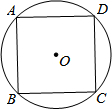
    5．如图，AC是矩形ABCD的对角线，将矩形纸片折叠，使点C与点A重合，请在图中画出折痕，然后再在图中画出矩形ABCD的外接圆．（用尺规作图，写出结论，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

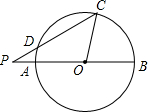    2．如图，已知AB是⊙O的直径，AB=16，点P是AB所在直线上一点，OP=10，点C是⊙O上一点，PC交⊙O于点D，sin∠BPC=$\frac{3}{5}$，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，在△ABC中，∠B=45°，∠C=30°，AC=2，点D在BC上，将△ACD沿直线AD翻折后，点C落在点E处，边AE交边BC于点F，如果DE∥AB，那么$\frac{CF}{BF}$的值是$\sqrt{3}$+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

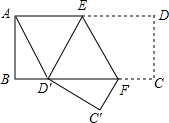    19．如图，四边形ABCD是矩形，AB=2，将矩形ABCD沿EF折叠，点D落在BC边的D′处．若四边形AD′FE恰好为菱形，则矩形的边AD的长度为$\frac{8\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．在△ABC中，∠BAC=90°，AD⊥BC于D，BG平分∠ABC交AD于E，交AC于G，GF⊥BC于F，连接EF．
    （1）如图1，求证：四边形AEFG是菱形；
    （2）如图2，若E为BG的中点，过点E作EM∥BC交AC于M，在不添加任何辅助线的情况下，请直接写出图2中是CM长$\sqrt{3}$倍的所有线段．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

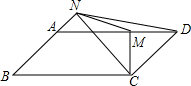    3．如图，在?ABCD中，AD=2AB，CM⊥AD，CN⊥AB，垂足分别为M、N，连接MN，ND．则下列结论一定正确的是①②③④．（请将序号在填在横线上）
    ①CN=2CM；
    ②∠NAD=∠NCM；
    ③S△NCD=$\frac{1}{2}$S四边形ABCD；
    ④AM2-AN2=3CM2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．（1）解不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1＜2-2x}\end{array}\right.$
    （2）如图，四边形ABCD是⊙O的内接正方形，若正方形的面积等于4，求⊙O的面积．

    查看答案和解析>>

    同步练习册答案