练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在如图所示的单位正方形网格中，△ABC（点B与原点O重合）经过平移后得到△A1B1C1，已知在AC上一点P（2.4，2）平移后的对应点为P1，点P1绕点O逆时针旋转180°，得到对应点P2，则P2点的坐标为（ ）

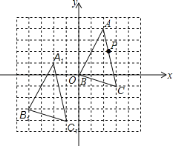
    A.（1.4，1）B.（1.5，2）C.（1.6，1）D.（2.4，1）

    【答案】C

    【解析】

    根据平移的性质得出，△ABC的平移方向以及平移距离，即可得出P1坐标，进而利用中心对称图形的性质得出P2点的坐标．

    解：∵A点坐标为：（2，4），A1（﹣2，1），

    ∴点P（2.4，2）平移后的对应点P1为：（﹣1.6，﹣1），

    ∵点P1绕点O逆时针旋转180°，得到对应点P2，

    ∴P2点的坐标为：（1.6，1）．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在疫情期间，某地推出线上名师公益大课堂，为广大师生、其他社会人士提供线上专业知识学习、心理健康疏导．参与学习第一批公益课的人数达到2万人，因该公益课社会反响良好，参与学习第三批公益课的人数达到2．42万人．参与学习第二批、第三批公益课的人数的增长率相同．

    （1）求这个增长率；

    （2）据大数据统计，参与学习第三批公益课的人数中，师生人数在参与学习第二批公益课的师生人数的基础上增加了80%；但因为已经部分复工，其他社会人士的人数在参与学习第二批公益课的其他社会人士人数的基础上减少了60%．求参与学习第三批公益课的师生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，AD=4，∠C=30°，⊙O与AD相交于点F，AB为⊙O的直径，⊙O与CD的延长线相切于点E，则劣弧FE的长为_________

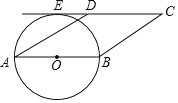
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】张老师将“校园诗词大赛”所有参赛选手的比赛成绩(得分均为整数)进行整理，并分别绘制成扇形统计图和频数直方图，部分信息如下：

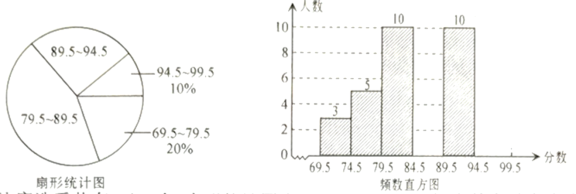
    （1）本次比赛选手共有_ 人，扇形统计图中“”这一组人数占总参赛人数的百分比为_ ，频数直方图中“”这一组的人数为__ ；

    （2）赛前规定，成绩由高到低前的参赛选手获奖某参赛选手的比赛成绩为分，试判断他能否获奖，并说明理由；

    （3）成绩前四名是名男生和名女生，若从他们中任选人作为全区“诗词大会”重点培训对象，试求恰好选中男女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．

    （1）求商场经营该商品原来一天可获利润多少元？

    （2）设后来该商品每件降价x元，，商场一天可获利润y元．

    ①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？

    ②求出y与x之间的函数关系式，结合题意写出当x取何值时，商场获利润不少于2160元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，一次函数y=mx+n（m≠0）的图象与反比例函数y=（k≠0）的图象交于第一、三象限内的A、B两点，与y轴交于点C，过点B作BM⊥x轴，垂足为M，BM=OM，OB=2，点A的纵坐标为4．

    （1）求该反比例函数和一次函数的解析式；

    （2）连接MC，求四边形MBOC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某医院医生为了研究该院某种疾病的诊断情况，需要调查来院就诊的病人的两个生理指标，，于是他分别在这种疾病的患者和非患者中，各随机选取20人作为调查对象，将收集到的数据整理后，绘制统计图如下：

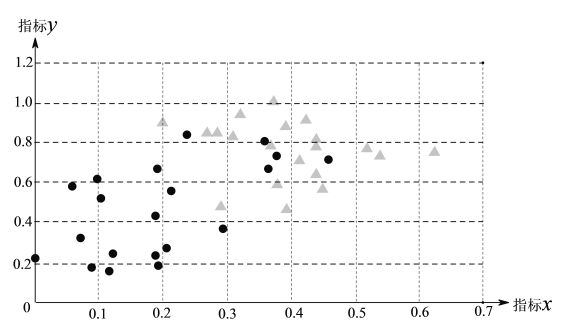
    注“●”表示患者，“▲”表示非患者．

    根据以上信息，回答下列问题：

    （1）在这40名被调查者中，

    ①指标低于0．4的有　　人；

    ②将20名患者的指标的平均数记作，方差记作，20名非患者的指标的平均数记作，方差记作，则 ， (填“>”，“=”或“<”)；

    （2）来该院就诊的500名未患这种疾病的人中，估计指标低于0．3的大约有 人；

    （3）若将“指标低于0．3，且指标低于0．8”作为判断是否患有这种疾病的依据，则发生漏判的概率多少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，E是CD边上一点（CE>DE），AE，BD交于点F．

    （1）如图1，过点F作GH⊥AE，分别交边AD，BC于点G，H．

    求证：∠EAB=∠GHC；

    （2）AE的垂直平分线分别与AD，AE，BD交于点P，M，N，连接CN．

    ①依题意补全图形；

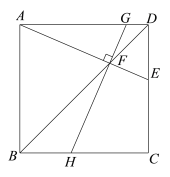
    图1 备用图

    ②用等式表示线段AE与CN之间的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD的对角线AC，BD相交于点O．E，F是AC上的两点，并且AE=CF，连接DE，BF．

    （1）求证：△DOE≌△BOF；

    （2）若BD=EF，连接DE，BF．判断四边形EBFD的形状，并说明理由．

    查看答案和解析>>

    同步练习册答案