

���� ��1���ȸ���ͼ1�����ε����ѧ��������������ͼ1������ν�ļҳ�80�˳���ͼ2������ν�ļҳ���ռ�İٷֱ�20%���ó���ε���ļҳ�������������ε����������=ѧ��������+�ҳ���������Ȼ�ҳ���������ȥ�ɺ�����ν�ļҳ���������Ϊ���Եļҳ��������Ӷ��ɲ�ȫͼ1��
��2�����ݼҳ��ġ��ɡ������ͣ�1��������ļҳ���������������ɡ��ҳ��İٷֱȣ����ɵõ���ʾ�ҳ����ɡ���Բ�ĽǵĶ�����
��3����4λ�ҳ�ΪA��B��C��D��С����С���ļҳ��ֱ�ΪA��B��������״ͼ���ɣ�
��� �⣺��1����ͼ1��֪��ε����ѧ���������ǣ�140+30+30=200�ˣ�
��ε���ļҳ��������ǣ�80��20%=400�ˣ�
���Ե������������200+400=600�ˣ�
���Եļҳ������ǣ�400-40-80=280�ˣ�
��ȫͼ1���£�
��2����ʾ�ҳ����ɡ���Բ�ĽǵĶ���Ϊ$\frac{40}{400}$��360=36�㣻
��3����3����С����С���ļҳ��ֱ���A��B��ʾ������һ���ҳ���C��ʾ������״ͼ���£�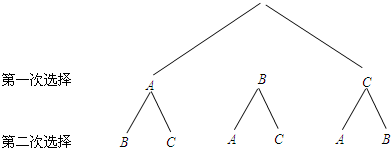
��ͼ��֪������6�ֵȿ��ܵĽ��������С����С���ļҳ���ͬʱѡ�е������2�֣�
����P��С����С���ҳ�ͬʱ��ѡ�У�=$\frac{2}{6}$=$\frac{1}{3}$��
���� ���⿼��������ͳ��ͼ������ͳ��ͼ�Լ����б�������״ͼ������ʣ���һ���ۺ��⣬Ҫ����ͼ�ۺϿ��飬���ɽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 0 | C�� | 2 | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m=2��n=3 | B�� | m=1��n=3 | C�� | m=4��n=3 | D�� | m=4��n=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2.2��10-5ǧ�� | B�� | 2.2��10-6ǧ�� | C�� | 2.17��10-5ǧ�� | D�� | 2.17��10-6ǧ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x1+x2=-3��x1•x2=-1 | B�� | x1+x2=-3��x1•x2=1 | ||
| C�� | x1+x2=3��x1•x2=-1 | D�� | x1+x2=3��x1•x2=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9��48-9��49 | B�� | 9��49-9��50 | C�� | 9��50-9��51 | D�� | 9��51-9��52 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b | B�� | a=b | C�� | a��b | D�� | a=$\frac{1}{b}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com