
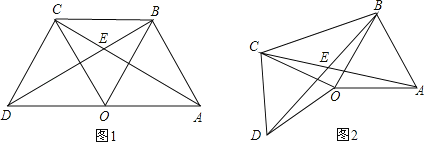
【题目】(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
【答案】(1)60°;(2)60°
【解析】试题分析:(1),由△DOC和△ABO都是等边三角形,且点O是线段AD的中点,可得OD=OC=OB=OA,∠1=∠2=60°,∠4=∠5,从而利用外角的性质可得∠AEB=∠4+∠6=∠4+∠5=∠2=60°;
(2)由△DOC和△ABO都是等边三角形,且点O是线段AD的中点,可得OD=OC=OB=OA,∠1=∠2=60°,∠4=∠5,∠6=∠7,根据三角形内角和可得∠5=∠6,从而利用外角的性质可得∠AEB=∠2+∠6﹣∠5=∠2+∠5﹣∠5=∠2.
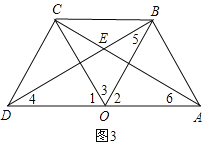
解:(1)如图3,
∵△DOC和△ABO都是等边三角形,
且点O是线段AD的中点,
∴OD=OC=OB=OA,∠1=∠2=60°,
∴∠4=∠5.
又∵∠4+∠5=∠2=60°,
∴∠4=30°.
同理∠6=30°.
∵∠AEB=∠4+∠6,
∴∠AEB=60°.
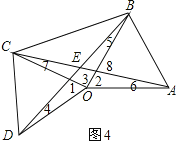
(2)如图4,
∵△DOC和△ABO都是等边三角形,
∴OD=OC,OB=OA,∠1=∠2=60°.
∴OD=OB,OA=OC,
∴∠4=∠5,∠6=∠7.
∵∠DOB=∠1+∠3,
∠AOC=∠2+∠3,
∴∠DOB=∠AOC.
∵∠4+∠5+∠DOB=180°,∠6+∠7+∠AOC=180°,
∴2∠5=2∠6,
∴∠5=∠6.
又∵∠AEB=∠8﹣∠5,∠8=∠2+∠6,
∴∠AEB=∠2+∠6﹣∠5=∠2+∠5﹣∠5=∠2,
∴∠AEB=60°.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两家商场进行促销活动,甲商场采用“满200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;……,乙商场按顾客购买商品的总金额打6折促销.
(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱?
(2)若顾客在甲商场购买商品的总金额为x(400≤x<600)元,优惠后得到商家的优惠率为p(p=![]() ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(200≤x<400)元,你认为选择哪家商场购买商品花钱较少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由方程3x-5=2x-4变形,得3x-2x=-4+5,这是根据什么变形的( )
A. 合并同类项法则B. 分配律C. 等式的基本性质1D. 等式的基本性质2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com