分析:(1)证AC是圆O1的切线,可连接O1A然后证O1A⊥PC即可,可通过∠PAO1是圆O2的内接四边形的外角来求解.
(2)证AD∥O1C,就是证∠PAD=∠O1CA,可通过与两角相等的中间角来求解;连接BA,那么∠O1BA就是与两角相等的中间角.(主要应用弦切角和圆周角定理来求解).
(3)由于BC,AC同与圆O1相切,因此根据切线长定理AC=BC,那么求BC也就是求AC的长,有了PD和⊙O1的半径即O1D,O1B的值,那么可根据切割线定理求出PA,由(2)得出的平行线,根据平行线分线段成比例定理,可得出关于PA,PC,PD,PO的比例关系,而PD,DQ1,PA的值都已知,因此可求出AC的长,也就求出了BC的长.
解答: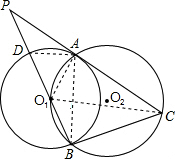
(1)证明:连接O
1A;
∵BC是⊙O
1的切线,
∴∠O
1BC=90°.
∵∠O
1AP是圆O
2的内接四边形的外角,
∴∠PAO
1=∠O
1BC=90°,
∴Q
1A⊥AC,
则AC是⊙O
1的切线.
(2)证明:连接AB,
∵PC切⊙O
1于点A,
∴∠PAD=∠ABD.
∵∠ACO
1=∠ABO
1,
∴∠PAD=∠ACO
1,
∴AD∥O
1C.
(3)解:∵PC是⊙O
1的切线,PB是⊙O
1的割线,
∴PA
2=PD•PB.
∵PD=1,PB=5,
∴PA=
,
∵PC是⊙O
1的切线.
又∵AD∥O
1C.
∴
=
.
∴
=
.
∴AC=2
.
∵AC,BC都是⊙O
1的切线,
∴BC=AC=2
.
点评:本题主要考查了切线的判定,切线长和切割线定理,圆周角定理等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

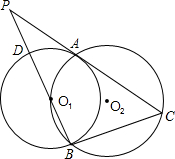 已知:如图,⊙O1与⊙O2相交于A、B两点,O1在⊙O2上,⊙O2的弦BC切⊙O1于B,延长BO1、CA交于点P、PB与⊙O1交于点D.
已知:如图,⊙O1与⊙O2相交于A、B两点,O1在⊙O2上,⊙O2的弦BC切⊙O1于B,延长BO1、CA交于点P、PB与⊙O1交于点D. (1)证明:连接O1A;
(1)证明:连接O1A;

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案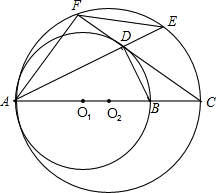 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.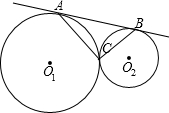 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=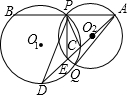 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且