
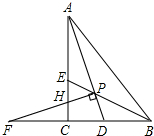
分析 (1)首先计算出∠APB=135°,进而得到∠BPD=45°,然后再计算出∠FPB=135°,然后证明△ABP≌△FBP,得∠F=∠CAD,然后证明△APH≌△FPD,进而得到AH=FD,再利用等量代换可得结论.
(2)由△ABP≌△FBP可得PA=PF.
(3)存在.m=2.由△ABP≌△FBP,△APH≌△FPD,得S△APB=S△FPB,S△APH=S△FPD,由HD∥EP,得S△EPH=S△EPD,只要证明S四边形ABDE=2S△ABP,即可解决问题.
解答 (1)证明:∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=$\frac{1}{2}$(∠CAB+∠CBA)=45°,
∴∠APB=135°,
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
在△ABP和△FBP中,
$\left\{\begin{array}{l}{∠ABP=∠PBF}\\{BP=BP}\\{∠APB=∠FPB}\end{array}\right.$,
∴△ABP≌△FBP(ASA),
∴∠BAP=∠F,
∵∠BAP=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
$\left\{\begin{array}{l}{∠APH=∠FPD}\\{PA=PF}\\{∠PAH=∠PFD}\end{array}\right.$,
∴△APH≌△FPD(ASA),
∴AH=FD,
又∵AB=FB,
∴AB=FD+BD=AH+BD.
(2)证明:由(1)可知△ABP≌△FBP,
∴PA=PF,
(3)存在.m=2.
理由:连接HD,ED.
∵△ABP≌△FBP,△APH≌△FPD,
∴S△APB=S△FPB,S△APH=S△FPD,PH=PD,
∵∠HPD=90°,
∴∠HDP=∠DHP=45°=∠BPD,
∴HD∥EP,
∴S△EPH=S△EPD,
∵S四边形ABDE=S△ABP+S△AEP+S△EPD+S△PBD
=S△ABP+(S△AEP+S△EPH)+S△PBD
=S△ABP+S△APH+S△PBD
=S△ABP+S△FPD+S△PBD
=S△ABP+S△FBP
=2S△ABP,
∴m=2.
点评 本题考查三角形综合题、全等三角形的判定和性质、角平分线的定义、平行线的性质,三角形的面积等知识,解题的关键是正确寻找全等三角形,学会利用平行线寻找面积相等的三角形,第三个问题有点难度,属于中考压轴题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在全民读书月活动中,某校随机调查了40名同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题,直接写出结果.
在全民读书月活动中,某校随机调查了40名同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题,直接写出结果.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
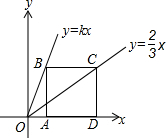 如图,点B、C分别在两条直线y=kx和y=$\frac{2}{3}$x上,点A、D是x轴上两点,已知四边形ABCD是正方形,则k值为$\frac{2}{5}$.
如图,点B、C分别在两条直线y=kx和y=$\frac{2}{3}$x上,点A、D是x轴上两点,已知四边形ABCD是正方形,则k值为$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com