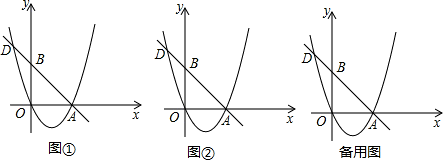
(1)解:y=-x+3,
当x=0时,y=3,
∴B(0,3),
把x=-1代入y=-x+3得:y=4,
∴D(-1,4),
当y=0时,0=-x+3,
∴x=3,
∴A(3,0),
∵抛物线过A(3,0),O(0,0),
把D(-1,4)代入y=ax
2+bx+c=a(x-0)(x-3)得:4=a(-1-0)(-1-3),
∴a=1,
∴y=(x-0)(x-3),
即抛物线的解析式是y=x
2-3x.
(2)解:设H(x,0),
则P(x,-x+3),Q(x,x
2-3x),
∴PH=-x+3,QH=3x-x
2,
∵x轴把△POQ分成两部分的面积之比为1:2,
∴

=

或

=2,
即

=

或

=2,
解得:x
1=2,x
2=3(舍去),x
3=3(舍去),x
4=

,
∴H点的坐标是(2,0)或(

,0).
(3)解:分为三种情况:
①若∠BAC=90°,设C(x,x
2-3x),
∵△AOB是等腰直角三角形,
∴∠BAO=45°,
∴∠OAC=45°,
∴tan∠OAC=1,
∴

=1,
解得:x
1=1,x
2=3(舍去),
∴C(1,-2);
②若∠ABC=90°时,
∵∠OBA=45°,
∴∠OBC=45°,
设直线BC交于x轴于E,其解析式是y=kx+3,
∴OE=OB=3,
∴E(-3,0),
代入得:0=-3k+3,
∴k=1,
∴y=k+3,
解方程组

得:

,

,
∴C(2+

,5-

)或(2-

,5-

);
③若∠ACB=90°时,设C(n,k),
AC
2+BC
2=AB
2,
即(n-3)
2+k
2+n
2+(k-3)
2=18,
n
2-3n+k
2-3k=0,
∵k=n
2-3n,
代入求出k
1=0,k
2=2,
∴n
2-3n=0,n
2-3n=2,
解得:n
1=0,n
2=3(舍去),n
3=

,n
4=

,
∴C(0,0)或(

,2)或(

,2),
综合上述:存在,点C的坐标是(1,-2)或(2+

,5+

)或(2-

,5-

)或(0,0)或(

,2)或(

,2).
分析:(1)求出B、D、A的坐标,把D的坐标代入y=a(x-0)(x-3)求出a即可;
(2)设H(x,0),得出P(x,-x+3),Q(x,x
2-3x),求出PH和QH,根据三角形的面积得出

=

和

=2,代入求出即可;
(3)分为三种情况:①若∠BAC=90°,设C(x,x
2-3x),tan∠OAC=1,代入求出即可;②若∠ABC=90°时,得出求出直线BC的解析式,和抛物线的解析式得出方程组,求出方程组的解即可;③若∠ACB=90°时,设C(n,k),根据勾股定理得出AC
2+BC
2=AB
2,代入得到(n-3)
2+k
2+n
2+(k-3)
2=18,求出即可.
点评:本题考查了三角形的面积,勾股定理,用待定系数法求出二次函数的解析式,等腰三角形的性质和判定等知识点的应用,主要考查学生运用这些性质进行计算的能力,本题难度偏大,对学生有较高的要求,分类讨论思想的运用.

 =
= 或
或 =2,
=2, =
= 或
或 =2,
=2, ,
, ,0).
,0). =1,
=1, 得:
得: ,
, ,
, ,5-
,5- )或(2-
)或(2- ,5-
,5- );
); ,n4=
,n4= ,
, ,2)或(
,2)或( ,2),
,2), ,5+
,5+ )或(2-
)或(2- ,5-
,5- )或(0,0)或(
)或(0,0)或( ,2)或(
,2)或( ,2).
,2). =
= 和
和 =2,代入求出即可;
=2,代入求出即可;

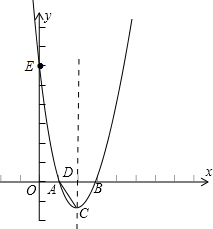 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线. 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=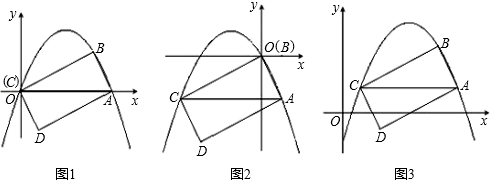
 如图,将抛物线y=-
如图,将抛物线y=-