
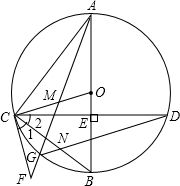
 (2013•遂宁)如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(2013•遂宁)如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.| 1 | 4 |
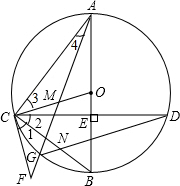 (1)证明:∵△BCO中,BO=CO,
(1)证明:∵△BCO中,BO=CO,| 1 |
| 4 |
| 1 |
| 4 |
| CO2-EO2 |
| 42-12 |
| 15 |
| CE2+AE2 |
(
|
| 10 |
| CE2+BE2 |
(
|
| 6 |
| 15 |
| CM |
| CN |
| AC |
| CD |
| 1 |
| 2 |
| 1 |
| 2 |
| CM•CD |
| AC |
2×2
| ||
2
|
| 6 |
| 6 |
| 6 |
| 6 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2013•遂宁)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
(2013•遂宁)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
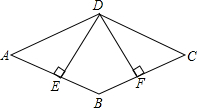 (2013•遂宁)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF.求证:
(2013•遂宁)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•遂宁)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是
(2013•遂宁)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com