
| A. | $\frac{AD}{DE}$=$\frac{DB}{EC}$ | B. | $\frac{AD}{AE}$=$\frac{EC}{BD}$ | C. | $\frac{AE}{AC}$=$\frac{AD}{AB}$ | D. | $\frac{AD}{EC}$=$\frac{AC}{BC}$ |
科目:初中数学 来源: 题型:选择题
| A. | $\frac{ED}{BC}$=$\frac{AD}{AB}$ | B. | $\frac{ED}{BC}$=$\frac{AD}{DB}$ | C. | $\frac{AD}{DB}$=$\frac{EC}{AE}$ | D. | $\frac{AD}{AE}$=$\frac{DB}{EC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某河堤迎水坡AB的坡比i=1:$\sqrt{3}$,堤高BC=5m,则坡面AB的长是( )
如图,某河堤迎水坡AB的坡比i=1:$\sqrt{3}$,堤高BC=5m,则坡面AB的长是( )| A. | 5 m | B. | 10m | C. | 15 m | D. | 5 m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
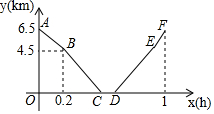 从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.其中正确的个数为( )
从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com