
方程x(x﹣2)+x﹣2=0的解为( )
A. x=2 B. x1=2,x2=1 C. x=﹣1 D. x1=2,x2=﹣1
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
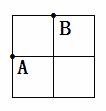
如图,在2×2的正方形网格中有9个格点,已经取定点A和点B,在余下的7个点中任取一点C,使△ABC为等腰直角三角形的概率是( )
A.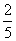 B.
B.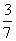 C.
C.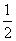 D.
D.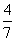
查看答案和解析>>
科目:初中数学 来源: 题型:
已知矩形ABCD中,AB=10cm,AD=4cm,作如下折叠操作.如图1和图2所示,在边AB上取点M,在边AD或边DC上取点P.连接MP.将△AMP或四边形AMPD沿着直线MP折叠得到△A′MP或四边形A′MPD′,点A的落点为点A′,点D的落点为点D′.
探究:
(1)如图1,若AM=8cm,点P在AD上,点A′落在DC上,则∠MA′C的度数为 ;
(2)如图2,若AM=5cm,点P在DC上,点A′落在DC上,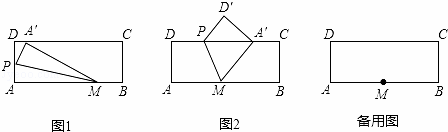
①求证:△MA′P是等腰三角形;
②直接写出线段DP的长.
(3)若点M固定为AB中点,点P由A开始,沿A﹣D﹣C方向.在AD,DC边上运动.设点P的运动速度为1cm/s,运动时间为ts,按操作要求折叠.
①求:当MA′与线段DC有交点时,t的取值范围;
②直接写出当点A′到边AB的距离最大时,t的值;
发现:
若点M在线段AB上移动,点P仍为线段AD或DC上的任意点.随着点M位置的不同.按操作要求折叠后.点A的落点A′的位置会出现以下三种不同的情况:
不会落在线段DC上,只有一次落在线段DC上,会有两次落在线段DC上.
请直接写出点A′由两次落在线段DC上时,AM的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
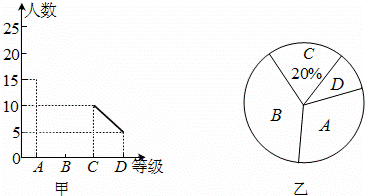
“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,将一张直角△ABC纸片折叠,使点A与点C重合,这时DE为折痕,△ECB为等腰三角形;继续将纸片沿△ECB的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样的矩形为“叠加矩形”.
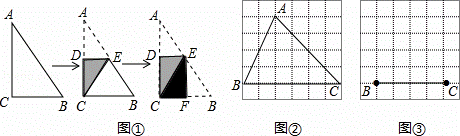
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕.
(2)如图③在正方形网格中,以给定的BC为一边,画出一个斜三角形△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形.
(3)若一个三角形所折成的“叠加矩形”为正方形,那么必须满足的条件是什么?
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com