
如图①,将一张直角△ABC纸片折叠,使点A与点C重合,这时DE为折痕,△ECB为等腰三角形;继续将纸片沿△ECB的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样的矩形为“叠加矩形”.
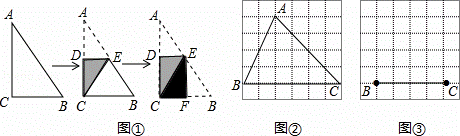
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕.
(2)如图③在正方形网格中,以给定的BC为一边,画出一个斜三角形△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形.
(3)若一个三角形所折成的“叠加矩形”为正方形,那么必须满足的条件是什么?
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是什么?
考点: 几何变换综合题.
分析: (1)图2中将三角形的三个角分别向三角形内部进行折叠即可;
(2)图3中只要使三角形一边上的高等于该边长即可;
(3)利用折叠后的两个重合的正方形可知,三角形一边长的一半和这一边上的高的一半都等于正方形的边长,所以三角形的一边和这边上的高应该相等;
(4)如果一个四边形能折叠成叠加矩形,可以将四边形的四个角分别向四边形内部折叠即可得到该结果,折痕应经过四边中点,而连接四边形各边中点得到矩形的话,该四边形的对角线应互相垂直.
解答: 解:(1)(2)

(3)一边长与该边上的高相等的直角三角形或锐角三角形;
(4)对角线互相垂直.
点评: 此题考查是几何变换问题,是一道操作题,一方面考查了学生的动手操作能力,另一方面考查了学生的空间想象能力,重视知识的发生过程,让学生体验学习的过程.关键是在操作的过程中,应善于分析图形,结合中点即可解决问题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
在△ABC中,AH⊥BC于点H,点P从B点开始出发向C点运动,在运动过程中,设线段AP的长为y,线段BP的长为x(如图1),而y关于x的函数图象如图2所示.Q (1,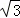 )是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=
)是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=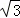 ;③AC=2
;③AC=2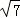 ;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是 (填写序号).
;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是 (填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
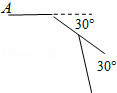
如图,王老师在上多边形外角和这节课时,做了一个活动,让小明在操场上从A点出发前进1m,向右转30°,再前进1m,又向右转30°,…,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.小明一共走了 m,这个多边形的内角和是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其它区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中,正确的是( )
A、相等的角是对顶角。 B、等腰三角形都相似。
C、位似图形上任意一对对应点到位似中心的距离之比等于位似比。
D、对角线互相垂直平分的四边形是正方形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com