
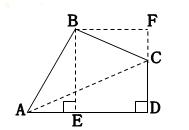
如图,四边形ABCD中,∠ABC=90°,CD⊥AD,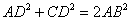 ,
,
(1)求证:AB=BC;
(2)过点B作BE⊥AD于E,若四边形ABCD的面积为 ,求BE的长.
,求BE的长.
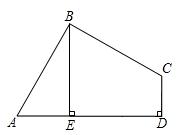
(1)连接AC ,由勾股定理得
,由勾股定理得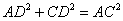 ,
,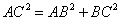 ,又
,又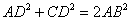 ,所以
,所以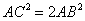 ,所以
,所以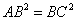 ,所以AB=BC.
,所以AB=BC.
(2)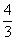 .
.
【解析】
试题分析:(1)连接AC,由勾股定理得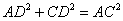 ,又
,又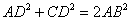 ,所以
,所以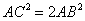 ,所以
,所以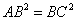 ,问题得证;
,问题得证;
(2)过点B作BF⊥BE,延长DC交BF于F,即可证得△ABE≌△CBF,则S四边形BEDF=S四边形ABCD= ,又四边形BEDF为正方形,则BE=
,又四边形BEDF为正方形,则BE=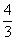 .
.
试题解析:(1)连接AC,由勾股定理得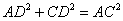 ,
,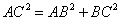 ,又
,又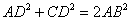 ,所以
,所以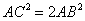 ,所以
,所以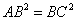 ,所以AB=BC.
,所以AB=BC.
(2)过点B作BF⊥BE,延长DC交BF于F,因为∠AEB=∠F,∠ABE=∠CBF,AB=BC,所以△ABE≌△CBF,所以BF=BE, 四边形BEDF为正方形,则S四边形BEDF=S四边形ABCD= ,又四边形BEDF为正方形,所以BE=
,又四边形BEDF为正方形,所以BE=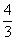 .
.
【难度】一般


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
小张利用休息日进行登山锻炼,从山脚到山顶的路程为12千米.他上午8时从山脚出发,到达山顶后停留了半小时,再原路返回,下午3时30分回到山脚.假设他上山与下山时都 是匀速行走,且下山比上山时的速度每小时快1千米,求小张上山时的速度.
是匀速行走,且下山比上山时的速度每小时快1千米,求小张上山时的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图:
甲、乙射击成绩统计表
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 0 | ||
| 乙 | 1 |


(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
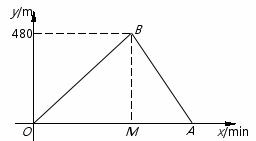
(1)A点所表示的实际意义是 ;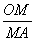 = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
某楼盘一楼是车库(暂不销售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款 (即贷款).
(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
(1)请写出每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式;
(2)小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
(3)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体的数据阐明你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
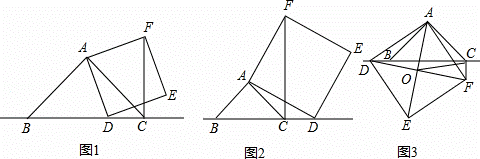

(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com