
【题目】如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)求证:△ACE≌△ABD;
(2)若AC=2,EC=4,DC=2![]() ,求∠ACD的度数;
,求∠ACD的度数;
(3)在(2)的条件下,直接写出DE的长为 .(只填结果,不用写计算过程)
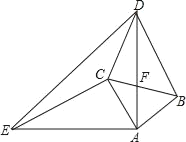
【答案】(1)证明见解析;(2)∠ACD=135°;(3)2![]() .
.
【解析】
(1)根据等腰直角三角形的性质可以得出∠EAC=∠DAB,再有AB=AC,AD=AE,根据SAS就可以得出结论;
(2)根据勾股定理可以求出BC的值为2![]() ,就可以得出BC=DC,在△BCD中由勾股定理的逆定理可以得出△BCD为等腰直角三角形,就可以得出∠BCD=90°,从而得出∠ACD的度数;
,就可以得出BC=DC,在△BCD中由勾股定理的逆定理可以得出△BCD为等腰直角三角形,就可以得出∠BCD=90°,从而得出∠ACD的度数;
(3)由(2)可以知道∠CDB=45°,而∠ABC=45°,就可以得出△ABD是直角三角形,由勾股定理就可以求出AB的值,再由勾股定理就可以求出DE的值.
解:(1)∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠EAC=∠BAD.
在△ACE和△ABD中,
 ,
,
∴△ACE≌△ABD(SAS);
(2)∵△ACE≌△ABD(SAS),
∴DB=EC=4,
在Rt△ABC中,AB2+AC2=BC2,
∴BC2=22+22=8,
在△DBC中,BC2+DC2=8+8=16=42=BD2,
∴∠DCB=90°,
∴∠ACD=90°+45°=135°;
(3)∵BC2=8,DC2=8,
∴BC=DC.
∵∠DCB=90°,
∴∠DBC=45°.
∵∠ABC=45°,
∴∠ABD=90°.
在Rt△ABD中由勾股定理,得:
![]() .
.
在Rt△AED中由勾股定理,得:
![]() .
.
故答案为:![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式x2﹣4>0
解:∵x2﹣4=(x+2)(x﹣2)
∴x2﹣4>0可化为
(x+2)(x﹣2)>0
由有理数的乘法法则“两数相乘,同号得正”,得
①![]() ②
②![]()
解不等式组①,得x>2,
解不等式组②,得x<﹣2,
∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2,
即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2.
解答下列问题:
(1)一元二次不等式x2﹣25>0的解集为 ;
(2)分式不等式![]() 的解集为 ;
的解集为 ;
(3)解一元二次不等式2x2﹣3x<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的对应点位置如图所示:
![]()
(1)化简:∣a∣+∣a+b∣-2∣a-b∣
(2)若a与-![]() 的距离等于b与-
的距离等于b与-![]() 的距离,求-3(a+b)+5的值.
的距离,求-3(a+b)+5的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
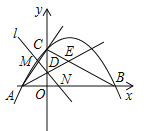
【题目】(2017南宁,第26题,10分)如图,已知抛物线![]() 与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时,![]() 均为定值,并求出该定值.
均为定值,并求出该定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )

A. (1007,1008) B. (1008,1007) C. (1006,1007) D. (1007,1006)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一根绳子对折后得到的图形为线段AB,从点P处把绳子剪断,已知AP:BP=4:5,若剪断后的各段绳子中最长的一段为80cm,则绳子的原长为________ cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角∠AOB,射线OC不与OA,OB重合,OM,ON分别平分∠AOC,∠BOC.

(1)当OC在∠AOB的内部
①若∠BOC=50°,∠AOC=20°,求∠MON的大小;
②若∠MON=30°,求∠AOB的大小;
(2)当射线OC在∠AOB外部,且∠AOB=80°,请直接写出∠MON的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿水青山就是金山银山,国家倡导全民植树。在今年3月12日植树节当天,某校七年级一班48名学生全部参加了植树活动,男生每人栽种4株,女生每人栽种3株,全班共栽种170株。
(1)该班男、女生各为多少人?
(2)学校选择购买甲、乙两种树苗,甲树苗![]() ,乙树苗
,乙树苗![]() .如果要使购买树苗的钱不超过1200元,那么最多可以购买甲树苗多少株?
.如果要使购买树苗的钱不超过1200元,那么最多可以购买甲树苗多少株?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com