
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
【答案】(1)每台电脑机箱、液晶显示器的进价各是60元,800元;
(2)利润最大为4400元.
【解析】
(1)设每台电脑机箱的进价是x元,液晶显示器的进价是y元,根据“若购进电脑机箱10台和液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液晶显示器5台,共需要资金4120元”即可列方程组求解;
(2)设购进电脑机箱z台,根据“可用于购买这两种商品的资金不超过22240元,所获利润不少于4100元”即可列不等式组求解.
解:(1)设每台电脑机箱、液晶显示器的进价各是x,y元,
根据题意得:![]() ,
,
解得:![]() ,
,
答:每台电脑机箱、液晶显示器的进价各是60元,800元;
(2)设该经销商购进电脑机箱m台,购进液晶显示器(50-m)台,
根据题意得:![]() ,
,
解得:24≤m≤26,
因为m要为整数,所以m可以取24、25、26,
从而得出有三种进货方式:①电脑箱:24台,液晶显示器:26台,
②电脑箱:25台,液晶显示器:25台;
③电脑箱:26台,液晶显示器:24台.
∴方案一的利润:24×10+26×160=4400,
方案二的利润:25×10+25×160=4250,
方案三的利润:26×10+24×160=4100,
∴方案一的利润最大为4400元.
答:该经销商有3种进货方案:①进24台电脑机箱,26台液晶显示器;②进25台电脑机箱,25台液晶显示器;③进26台电脑机箱,24台液晶显示器.第①种方案利润最大为4400元.


科目:初中数学 来源: 题型:
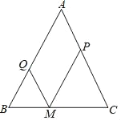
【题目】已知:在△ABC中,AB=AC=5,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
(1)求四边形AQMP的周长;
(2)M位于BC的什么位置时,四边形AQMP为菱形?指出点M的位置,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
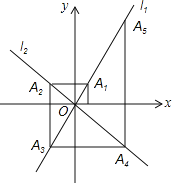
【题目】如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过A1点作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2019的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AE是ΔABC的角平分线,AD是BC边上的高。若∠ABC=34°,∠ACB=64°,则∠DAE的大小是( )
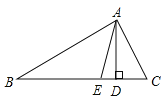
A. 5°B. 13°C. 15°D. 20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y=![]() 的图象上,且sin∠BAC=
的图象上,且sin∠BAC=![]() .
.
(1)求k的值和边AC的长;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
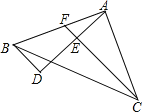
A. 6B. 5C. 4D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=2,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com