
【题目】已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y=![]() 的图象上,且sin∠BAC=
的图象上,且sin∠BAC=![]() .
.
(1)求k的值和边AC的长;
(2)求点B的坐标.
【答案】(1) k的值和边AC的长分别是:3,5.(2) 点B的坐标是(-![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
试题分析:(1)本题需先根据C点的坐标在反比例函数y=![]() 的图象上,从而得出k的值,再根据且sin∠BAC=
的图象上,从而得出k的值,再根据且sin∠BAC=![]() ,得出AC的长.
,得出AC的长.
(2)本题需先根据已知条件,得出∠DAC=∠DCB,从而得出CD的长,根据点B的位置即可求出正确答案.
试题解析:(1)∵点C(1,3)在反比例函数y=![]() 的图象上,
的图象上,
∴3=![]() ,解得k=3,
,解得k=3,
∵sin∠BAC=![]()
∴sin∠BAC=![]() =
=![]()
∴AC=5;
∴k的值和边AC的长分别是:3,5.
(2)①当点B在点A右边时,如图,
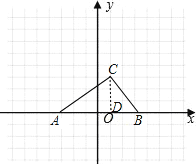
作CD⊥x轴于D.
∵△ABC是直角三角形,
∴∠DAC=∠DCB,
又∵sin∠BAC=![]() ,
,
∴tan∠DAC=![]() ,
,
∴![]() ,
,
又∵CD=3,
∴BD=![]() ,
,
∴OB=1+![]() =
=![]() ,
,
∴B(![]() ,0);
,0);
②当点B在点A左边时,如图,
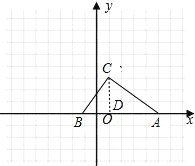
作CD⊥x轴于D.
∵△ABC是直角三角形,
∴∠B+∠A=90°,∠B+∠BCD=90°,
∴∠DAC=∠DCB,
又∵sin∠BAC=![]() ,
,
∴tan∠DAC=![]() ,
,
∴![]() ,
,
又∵CD=3,
∴BD=![]() ,BO=BD-1=
,BO=BD-1=![]() ,
,
∴B(-![]() ,0)
,0)
∴点B的坐标是(-![]() ,0),(
,0),(![]() ,0).
,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )

A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面内有两点A(0,2)、B(﹣2,0)、C(2,0).
(1)△ABC的形状是 等腰直角三角形;
(2)求△ABC的面积及AB的长;
(3)在y轴上找一点P,如果△PAB是等腰三角形,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
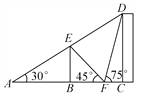
【题目】如图,楼房CD旁边有一池塘,池塘中有一电线杆BE高10米,在池塘边F处测得电线杆顶端E的仰角为45°,楼房顶点D的仰角为75°,又在池塘对面的A处,观测到A,E,D在同一直线上时,测得电线杆顶端E的仰角为30°.
(1)求池塘A,F两点之间的距离;
(2)求楼房CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于依次排列的多项式x+a,x+b,x+c,x+d(a,b,c,d是常数),当它们满足在![]() ,且M为常数时,则称a,b,c,d是一组平衡数,M是该组平衡数的平衡因子,例如:对于多项式x+2,x+1,x+6,x+5,因为
,且M为常数时,则称a,b,c,d是一组平衡数,M是该组平衡数的平衡因子,例如:对于多项式x+2,x+1,x+6,x+5,因为![]() ,所以2,1,6,5是一组平衡数,4是该组平衡数的平衡因子.
,所以2,1,6,5是一组平衡数,4是该组平衡数的平衡因子.
(1)已知2,4,7,9是一组平衡数,求该组平衡数的平衡因子M;
(2)若a,b,c,d是一组平衡数,a=-4,d=3,请直接写出组b,c的值;
(3)当a,b,c,d之间满是什么数量关系时,它们是一组平衡数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
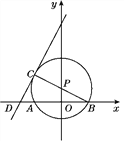
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划用3300元购进甲,乙两种商品共100个,这两种商品的进价、售价如下表:
进价(元/个) | 售价(元/个) | |
甲种 | 25 | 30 |
乙种 | 45 | 60 |
(1)求甲、乙两种商品各进多少个?
(2)全部售完100个商品后,该商场获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com