
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
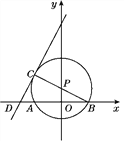
【答案】(1)C(-2,2);(2)证明见解析.
【解析】试题分析:
(1)Rt△OBP中,由勾股定理得到OP的长,连接AC,因为BC是直径,所以∠BAC=90°,因为OP是△ABC的中位线,所以OA=2,AC=2,即可求解;
(2)由点C的坐标可得直线CD的解析式,则可求点D的坐标,从而可用SAS证△DAC≌△POB,进而证∠ACB=90°.
试题解析:
(1)解:如图,连接CA.∵OP⊥AB,∴OB=OA=2.∵OP2+BO2=BP2,
∴OP2=5-4=1,OP=1.∵BC是⊙P的直径,∴∠CAB=90°.
∵CP=BP,OB=OA,∴AC=2OP=2.∴B(2,0),P(0,1),C(-2,2).
(2)证明:∵直线y=2x+b过C点,∴b=6.∴y=2x+6.
∵当y=0时,x=-3,∴D(-3,0).∴AD=1.∵OB=AC=2,AD=OP=1,
∠CAD=∠POB=90°,∴△DAC≌△POB.∴∠DCA=∠ABC.
∵∠ACB+∠CBA=90°,∴∠DCA+∠ACB=90°,即CD⊥BC.∴CD是⊙P的切线.


科目:初中数学 来源: 题型:
【题目】已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y=![]() 的图象上,且sin∠BAC=
的图象上,且sin∠BAC=![]() .
.
(1)求k的值和边AC的长;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
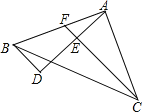
A. 6B. 5C. 4D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(甲)是四边形纸片 ABCD,其中∠B=130°,∠D=50°.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门).安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离.假设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )
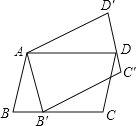
A. 105°B. 170°C. 155°D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=2,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行统计,并绘制出了如图1和图2所示的统计图,根据图中信息解答下列问题:

(1)这天共销售了多少个粽子?
(2)销售B品牌粽子多少个?并补全图1中的条形图;
(3)求出A品牌粽子在图2中所对应的圆心角的度数;
(4)根据上述统计信息,明年端午节期间该商场对A、B、C三种品牌的粽子如何进货?请你提一条合理化的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com