
【题目】已知:在△ABC中,AB=AC=5,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
(1)求四边形AQMP的周长;
(2)M位于BC的什么位置时,四边形AQMP为菱形?指出点M的位置,并加以证明.
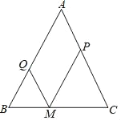
【答案】(1)四边形AQMP的周长=10;(2)点M位于BC的中点时,四边形AQMP是菱形.理由见解析.
【解析】
(1)根据有两组对边分别平行的四边形是平行四边形证明即可;
(1)根据平行四边形的性质可得到对应角相等对应边相等,从而不难求得其周长.
(1)∵AB∥MP,QM∥AC,∴四边形APMQ是平行四边形,∴AQ=MP,QM=AP.
∵AB=AC,∴∠B=∠C.
∵∠B=∠PMC,∠C=∠QMB,∴∠PMC=∠QMB,∴BQ=QM,PM=PC,∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=10.
(2)点M位于BC的中点时,四边形AQMP是菱形.理由如下:
∵BM=MC,PM∥AB,MQ∥AC,∴AP=PC,AQ=BQ,∴PM![]() AB,MQ
AB,MQ![]() AC.
AC.
∵AB=AC,∴MP=MQ.
∵四边形AQMP是平行四边形,∴四边形AQMP是菱形.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+220的值.
解:设S=1+2+22+23+24+…+220,将等式两边同时乘以2得:2S=2+22+23+24+25+…+221
将下式减去上式得2S﹣S=221﹣1
即S=221﹣1
即1+2+22+23+24+…+220=221﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+22016
(2)1+2+22+23+24+…+2n(其中n为正整数)
(3)1+5+52+53+54+…+5n(其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-1,3),点B(-1,-4),若常数a使得一次函数y=ax+1与线段AB有交点,且使得关于x的不等式组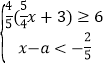 无解,则所有满足条件的整数a的个数为( )
无解,则所有满足条件的整数a的个数为( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,直线y1=﹣![]() x+3与x轴、y轴分别交于A、B两点,直线y2=﹣2x+b经过点A,已知点C(﹣1,0),直线BC与直线y2相交于点D.
x+3与x轴、y轴分别交于A、B两点,直线y2=﹣2x+b经过点A,已知点C(﹣1,0),直线BC与直线y2相交于点D.
(1)请直接写出:A点坐标为 ,直线BC解析式为 ,D点坐标为 ;
(2)若线段OA在x轴上移动,且点O,A移动后的对应点为O1、A1,首尾顺次连接点O1、A1、D、B构成四边形O1A1DB,当四边形O1A1DB的周长最小时,y轴上是否存在点M,使|A1M﹣DM|有最大值,若存在,请求出此时M的坐标;若不存在请说明理由.
(3)如图3,过点D作DE∥y轴,与直线AB交于点E,若Q为线段AD上一动点,将△DEQ沿边EQ翻折得到直线AB上方的△D′EQ,是否存在点Q使得△D′EQ与△AEQ的重叠部分图形为直角三角形,若存在,请求出DQ的长;若不存在,请说明理由.
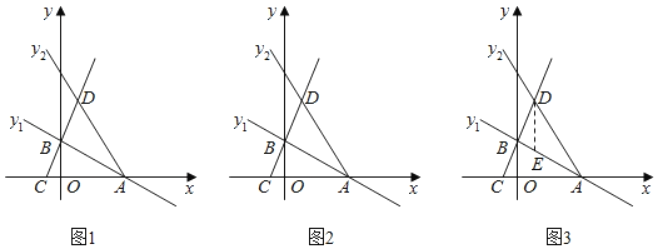
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要将本公司100吨货物运往某地销售,经与运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨,已知租用1辆甲型汽车和2辆乙型汽车共需费用2600元;租用2辆甲型汽车和1辆乙型汽车共需费用2500元,且同一型号汽车每辆租车费用相同.
(1)求租用辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若这个公司计划此次租车费用不超过5200元,通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )

A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.
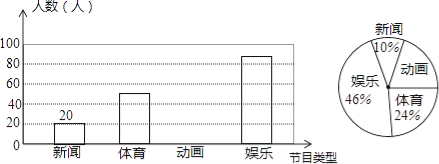
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com