【题目】阅读材料：求1+2+22+23+24+…+220的值．
解：设S=1+2+22+23+24+…+220，将等式两边同时乘以2得：2S=2+22+23+24+25+…+221
将下式减去上式得2S﹣S=221﹣1
即S=221﹣1
即1+2+22+23+24+…+220=221﹣1
请你仿照此法计算：
（1）1+2+22+23+24+…+22016
（2）1+2+22+23+24+…+2n（其中n为正整数）
（3）1+5+52+53+54+…+5n（其中n为正整数）
【答案】（1）22017﹣1；（2）2n+1﹣1；（3）
.
【解析】
（1）设原式=S，两边乘以2变形得到关系式，两式相减即可求出S；
（2）设原式=S，两边乘以2变形得到关系式，两式相减即可求出S；
（3）设原式=S，两边乘以5变形得到关系式，两式相减即可求出S．
解：（1）设S=1+2+22+23+24+…+22016，
两边乘以2得：2S=2+22+23+24+…+22027，
下式减去上式得：S=22017﹣1；
（2）设S=1+2+22+23+24+…+2n
两边乘以2得：2S=2+22+23+24+…+2n+1，
下式减去上式得：S=2n+1﹣1；
（3）设S=1+5+52+53+54+…+5n，
两边乘以5得：5S=5+52+53+54+…+5n+1，
下式减去上式得：4S=5n+1﹣1，即S=，
则1+5+52+53+54+…+5n=．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】直线AB：y=﹣x+b分别与x，y轴交于A（6，0）、B 两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．
(1)求点B的坐标．
(2)求直线BC的解析式．
(3)直线 EF 的解析式为y=x，直线EF交AB于点E，交BC于点 F，求证：S△EBO=S△FBO．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE.以下四个结论：
①BD=CE；②∠ACE+∠DBC=45°；③BD⊥CE；④∠BAE+∠DAC=180°.其中结论正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，若
，是
.
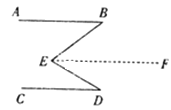
理由：如图，过点
作
，
则
.(依据)
因为，
所以
，
所以
.
所以
.
(1)上述证明过程中的依据是指 .
(2)若将点移至图2所示的位置，，此时
之间有什么关系？请说明理由.
(3)在图中，，
与
又有何关系？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小丽为了测旗杆AB的高度，小丽眼睛距地图1.5米，小丽站在C点，测出旗杆A的仰角为30o，小丽向前走了10米到达点E，此时的仰角为60o，求旗杆的高度。
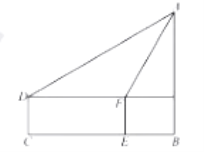
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，A、B是两座现代化城市，C是一个古城遗址，C城在A城的北偏东30°，在B城的北偏西45°，且C城与A城相距120千米，B城在A城的正东方向，以C为圆心，以60千米为半径的圆形区域内有古迹和地下文物，现要在A、B两城市修建一条笔直的高速公路．
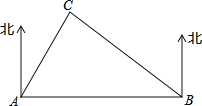
（1）请你计算公路的长度（保留根号）；
（2）请你分析这条公路有没有可能对文物古迹造成损毁，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
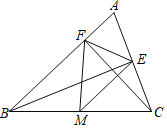
【题目】如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点，BC=10．
(1)若∠ABC=50°，∠ACB=60°，求∠EMF的度数；
(2)若EF=4，求△MEF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是
A．AB∥DC，AD∥BC B．AB=DC，AD=BC
C．AO=CO，BO=DO D．AB∥DC，AD=BC
查看答案和解析>>
科目：初中数学 来源： 题型：
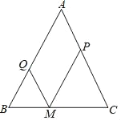
【题目】已知：在△ABC中，AB＝AC＝5，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．
（1）求四边形AQMP的周长；
（2）M位于BC的什么位置时，四边形AQMP为菱形？指出点M的位置，并加以证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com