
【题目】如图,若![]() ,是
,是![]() .
.
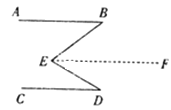
理由:如图,过点![]() 作
作![]() ,
,
则![]() .(依据)
.(依据)
因为![]() ,
,
所以![]() ,
,
所以![]() .
.
所以![]() .
.
(1)上述证明过程中的依据是指 .
(2)若将点![]() 移至图2所示的位置,
移至图2所示的位置,![]() ,此时
,此时![]() 之间有什么关系?请说明理由.
之间有什么关系?请说明理由.

(3)在图中,![]() ,
,![]() 与
与![]() 又有何关系?
又有何关系?

【答案】(1)两直线平等,内错角相等;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)根据两直线平行内错角相等即可得出∠B=∠BEF;
(2)过点E作EF∥AB,由平行线的性质可知∠B+∠BEF=180°,∠D+∠DEF=180°,再由角之间的关系即可得出结论;
(3)过点F作FM∥AB,用(1)的结论可知∠E=∠B+∠EFM,∠G=∠GFM+∠D,再由角之间的关系即可得出结论.
(1)过点E作EF∥AB,
则∠B=∠BEF(两直线平行内错角相等),
故答案为两直线平行内错角相等;
(2)过点E作EF∥AB,如图2所示.

∵AB∥EF,
∴∠B+∠BEF=180°,
∵EF∥AB∥CD,
∴∠D+∠DEF=180°,
∴∠B+∠BEF+∠D+∠DEF=180°+180°,
∵∠E=∠BEF+∠DEF,
∴∠B+∠D+∠E=360°.
(3)过点F作FM∥AB,如图3所示.

∵AB∥FM,结合(1)结论,
∴∠E=∠B+∠EFM,
∵FM∥AB∥CD,结合(1)结论,
∴∠G=∠GFM+∠D,
又∵∠F=∠EFM+∠GFM,
∴∠E+∠G=∠B+∠D+∠F.


科目:初中数学 来源: 题型:
【题目】某文具店有单价为10元、15元和20元的三种文具盒出售,该商店统计了2014年3月份这三种文具盒的销售情况,并绘制统计图(不完整)如下:

(1)这次调查中一共抽取了多少个文具盒?
(2)求出图1中表示“15元”的扇形所占圆心角的度数;
(3)在图2中把条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人同时登山,甲乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是 米/分钟,乙在A地提速时距地面的高度b为 米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请求出乙提速后y和x之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时乙距A地的高度为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于52棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°;
①求∠OCE的度数. ②若⊙O的半径为 ![]() ,求线段CF的长.
,求线段CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+220的值.
解:设S=1+2+22+23+24+…+220,将等式两边同时乘以2得:2S=2+22+23+24+25+…+221
将下式减去上式得2S﹣S=221﹣1
即S=221﹣1
即1+2+22+23+24+…+220=221﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+22016
(2)1+2+22+23+24+…+2n(其中n为正整数)
(3)1+5+52+53+54+…+5n(其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
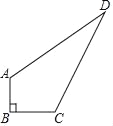
【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com