
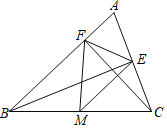
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,BC=10.
(1)若∠ABC=50°,∠ACB=60°,求∠EMF的度数;
(2)若EF=4,求△MEF的面积.
【答案】(1)∠EMF=40°;(2)2![]() .
.
【解析】
(1)根据直角三角形的性质得到BM=FM,根据等腰三角形的性质、三角形内角和定理计算;
(2)作MN⊥EF于N,根据直角三角形的性质得到FM=![]() BC=5,根据等腰三角形的性质、三角形面积公式计算.
BC=5,根据等腰三角形的性质、三角形面积公式计算.
解:(1)∵CF⊥AB,M为BC的中点,
∴BM=FM,
∵∠ABC=50°,
∴∠MFB=∠MBF=50°,
∴∠BMF=180°-2×50°=80°,
同理,∠CME═180°-2×60°=60°,
∴∠EMF=180°-∠BMF-∠CME=40°;
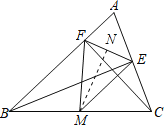
(2)作MN⊥EF于N,
∵CF⊥AB,M为BC的中点,
∴MF是Rt△BFC斜边上的中线,
∴FM=![]() BC=5,
BC=5,
同理可得,ME=5,
∴△EFM是等腰三角形,
∵EF=4,
∴FN=2,
∴MN=![]() =
=![]() ,
,
∴△EFM的面积=![]() EFMN=
EFMN=![]() ×4×
×4×![]() =2
=2![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°;
①求∠OCE的度数. ②若⊙O的半径为 ![]() ,求线段CF的长.
,求线段CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+220的值.
解:设S=1+2+22+23+24+…+220,将等式两边同时乘以2得:2S=2+22+23+24+25+…+221
将下式减去上式得2S﹣S=221﹣1
即S=221﹣1
即1+2+22+23+24+…+220=221﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+22016
(2)1+2+22+23+24+…+2n(其中n为正整数)
(3)1+5+52+53+54+…+5n(其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
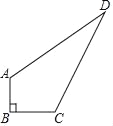
【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,过点A作直线DE,且满足BD⊥DE于点D,CE⊥DE于点E,当B,C在直线DE的同侧时,
(1)求证:DE=BD+CE;
(2)如果上面条件不变,当B,C在直线DE的异侧时,如图2,问BD、DE、CE之间的数量关系如何?写出结论并证明
(3)如果上面条件不变,当B,C在直线DE的异侧时,如图3,问BD、DE、CE之间的数量关系如何?写出结论并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-1,3),点B(-1,-4),若常数a使得一次函数y=ax+1与线段AB有交点,且使得关于x的不等式组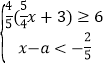 无解,则所有满足条件的整数a的个数为( )
无解,则所有满足条件的整数a的个数为( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )

A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com