
����Ŀ��ij�̳�������Ϊ2000Ԫ�ı�����2400Ԫ�۳���ƽ��ÿ�����۳�8̨��Ϊ����Ϲ��ҡ��ҵ����硱���ߵ�ʵʩ���̳�������ȡ�ʵ��Ľ��۴�ʩ.������������ֱ�����ۼ�ÿ����50Ԫ��ƽ��ÿ����ܶ��۳�4̨��
��1������ÿ̨���併��xԪ���̳�ÿ���������ֱ����������yԪ����д��y��x֮��ĺ�������ʽ������Ҫ��д�Ա�����ȡֵ��Χ��
��2���̳�Ҫ�������ֱ���������ÿ��ӯ��4800Ԫ��ͬʱ��Ҫʹ���յõ�ʵ�ݣ�ÿ̨����Ӧ���۶���Ԫ��
��3��ÿ̨���併�۶���Ԫʱ���̳�ÿ���������ֱ����������ߣ���������Ƕ��٣�
���𰸡���1��y=-![]() x2+24x+3200��
x2+24x+3200��
��2��ÿ̨����Ӧ����200Ԫ��
��3��ÿ̨������ۼ۽���150Ԫʱ���̳�������������������5000Ԫ��
�����������������(1)������������=���������������ó�������ϵʽ��(2)����������ó����̣�Ȼ�������⣻(3)�������κ����䷽�ɶ���ʽ��Ȼ����м���.
���������(1)���������⣬��y=��2400-2000-x����8+4��![]() ���� ��y=-
���� ��y=-![]() +24x+3200��
+24x+3200��
(2)�������⣬��-![]() +24x+3200=4800����������
+24x+3200=4800����������![]() -300x+20000=0����������̣���
-300x+20000=0����������̣���![]() =100��
=100�� ![]() =200��
=200��
Ҫʹ���յõ�ʵ�ݣ�ȡx=200�����ԣ�ÿ̨����Ӧ����200Ԫ��
(3)������y=-![]() +24x+3200=-
+24x+3200=-![]() +5000��
+5000��
��ÿ̨������ۼ۽���150Ԫʱ���̳�������������������5000Ԫ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB��60���ף�
(1)��P���߶�AB��A����B����4����/�ֵ��ٶ��˶���ͬʱ��Q���߶���B����A����6����/�ֵ��ٶ��˶��������Ӻ�P��Q����������
(2)�����Ӻ�P��Q�������20���ף�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ������Լ��ˮ��ˮ��ʵ�н��ݼƷ��������շѱ�������
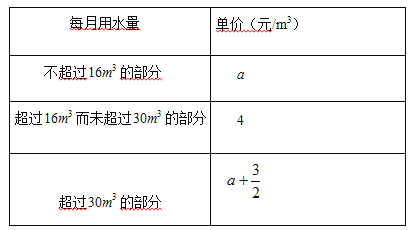
��1����ij�û�������ˮ22m3����Ӧ��ˮ��_____Ԫ���ú�a�Ĵ���ʽ��ʾ����
��2����ij�û�������ˮ36m3����ˮ��131Ԫ����a��
��3������2��������������ÿ����ˮ��xm3����ֱ����x�Ĵ���ʽ��ʾÿ��֧����ˮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ� ��
A.����������ľ���ֵ��ȣ���ô�����������
B.����������������
C.��Ϊ�෴�����������ľ���ֵ���
D.����������0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˾������ij������Ӫ��ȫ���ڶ�������Ľ��·�Ͻ��У�����涨��Ϊ��������Ϊ���������������г���̣���λ��km�����£�+8��+4����10����3��+6����5����2����7��+4��+6����9����11��
��1�����ڼ����˿��͵�Ŀ�ĵ�ʱ�������պûص���������㣿
��2�������һ���˿��͵�Ŀ�ĵ�ʱ������������������Զ��
��3��������������Ϊÿ��ʻ100km��������7L�����������������Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У��Ƿ��̵ĸ���Ϊ�� ��
��1����3��3����7 ��2��3x��5��2x��1 ��3��2x��6
��4��x��y��0 ��5��a��b>3 ��6��a2��a��6��0
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪����������A��B��Ӧ�����ֱ�Ϊ��2��5����PΪ�����ϵ�һ���㣬���Ӧ����Ϊx��
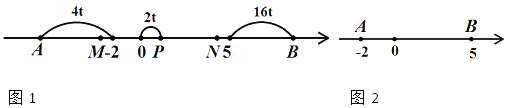
��1��PA= ��PB= ���ú�x��ʽ�ӱ�ʾ��
��2�����������Ƿ���ڵ�P��ʹPA+PB=10�������ڣ���ֱ��д��x��ֵ���������ڣ���˵�����ɣ�
��3����ͼ2����P��2����λ/s���ٶȴӵ�O�����˶���ͬʱ��A��4����λ/s���ٶ������˶�����B��16����λ/s���ٶ������˶������˶������У�M��N�ֱ���AP��OB���е㣬�ʣ� ![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ� ��
A. ������1.8��1.80��ʾ�����岻ͬ B. 0.0200��ȷ�����λ
C. 2.0��ȷ����λ D. 1.0��104��ȷ��ǧλ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com