
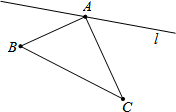
 如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?
如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等? 分析 分类讨论:当点P在BA上,点Q在AC上,如图1,则PB=2t,CQ=3t,AP=22-2t,AQ=28-3t,利用三角形全等得PA=AQ,即22-2t=28-3t;当点P、Q都在AB上,即P点和Q点重合时,△PFA与△QAG全等,此时2t+3t-28=22,当点P在AC上,点Q在AB上,如图2,则PA=2t-22,AQ=3t-28,由PA=AQ,即2t-22=3t-28;当点Q停在点B处,点P在AC上,由PA=QA得2t-22=22,然后分别解方程求出t,再根据题意确定t的值.
解答 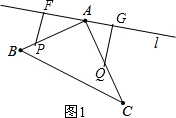 解:设P、Q点运动的时间为t,
解:设P、Q点运动的时间为t,
(1)当点P在BA上,点Q在AC上,如图1,
则PB=2t,CQ=3t,AP=22-2t,AQ=28-3t,
∵△PFA与△QAG全等,
∴PA=AQ,即22-2t=28-3t,解得t=6,
即P运动6秒时,△PFA与△QAG全等;
(2)当点P、Q都在AB上,即P点和Q点重合时,△PFA与△QAG全等,
此时2t+3t-28=22,
解得t=10,
(3)当点P在AC上,点Q在AB上,如图2,
则PA=2t-22,AQ=3t-28,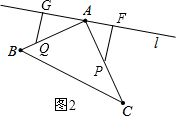 ∵△PFA与△QAG全等,
∵△PFA与△QAG全等,
∴PA=AQ,即2t-22=3t-28,解得t=6,舍去;
即P运动6秒时,△PFA与△QAG全等,
当点Q停在点B处,点P在AC上,由PA=QA得2t-22=22,解得t=22,舍去.
综上所述:当t等于6秒或10秒时,△PFA与△QAG全等.
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.对于动点问题常利用代数的方法解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
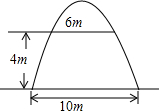 如图,某旅游景点的入口是一抛物线形拱门,它在地面上的水平宽度为10米,两侧距离地面4米高处各有一挂横匾用的铁环,两铁环间的水平距离为6米,则该拱门最高处到地面的距离为$\frac{25}{4}$米.
如图,某旅游景点的入口是一抛物线形拱门,它在地面上的水平宽度为10米,两侧距离地面4米高处各有一挂横匾用的铁环,两铁环间的水平距离为6米,则该拱门最高处到地面的距离为$\frac{25}{4}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
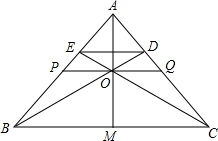 如图,已知:△ABC中,M为BC边的中点,O为AM上一点,BO的延长线交AC于点D,CO延长线交AB于点E,PQ∥BC,且PQ过点O与AB、AC分别交于P和点Q,求证:
如图,已知:△ABC中,M为BC边的中点,O为AM上一点,BO的延长线交AC于点D,CO延长线交AB于点E,PQ∥BC,且PQ过点O与AB、AC分别交于P和点Q,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com