
分析 (1)设购进甲种商品x件,乙种商品y件,根据销售问题的数量关系建立方程组求出其解即可;
(2)由购进甲种商品x件,则购进乙种商品(200一x)件,由利润等于售价-进价建立函数关系式就可以得出结论;
(3)根据一次函数的性质即可得到结论.
解答 解:(1)设购进甲种商品x件,乙种商品y件,由题意,得
$\left\{\begin{array}{l}{120x+100y=36000}\\{(130-120)x+(150-100)y=6000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=240}\\{y=72}\end{array}\right.$
答:该商场购进甲种商品240件,乙种商品72件.
(2)已知购进甲种商品x件,则购进乙种商品(200一x)件,根据题意,得
W=(130-120)x+(150-100)(200-x)=-40x+10000,
(3)∵k=-40<0,
∴W随x的增大而减小.
∴当购进甲种商品的件数为100件时利润最大,
∴进货方案为购进甲、乙种商品的件数各为100件,利润最大,
最大利润=-40×100+10000=9600元.
点评 本题考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,一次函数的性质的运用,解答时根据方程组的解求函数的解析式是关键.


科目:初中数学 来源: 题型:选择题
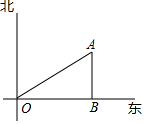 如图,小颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )
如图,小颖家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的400米处,那么水塔所在的位置到公路的距离AB是( )| A. | 200米 | B. | 200$\sqrt{3}$米 | C. | $\frac{400}{3}$$\sqrt{3}$米 | D. | 400$\sqrt{2}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
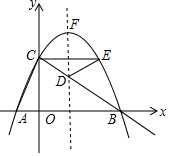 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴从左到右交于点A、B,与y轴交于点C
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴从左到右交于点A、B,与y轴交于点C查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 24 | C. | 32 | D. | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com