
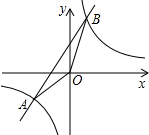
 如图,已知A(-2,-2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-2,-2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=| m |
| x |
| m |
| x |
| m |
| x |
| 4 |
| x |
| 4 |
| x |
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
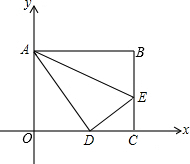 如图,平面直角坐标系中,矩形OABC的顶点B(10,8),点A在y轴上,点C在x轴上,E为BC上一点,把△ABE沿ZE折叠,点B落在OC上的D处.
如图,平面直角坐标系中,矩形OABC的顶点B(10,8),点A在y轴上,点C在x轴上,E为BC上一点,把△ABE沿ZE折叠,点B落在OC上的D处.| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
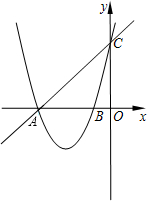 如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k-1图象过点A和点C,抛物线与x轴的另一交点是B,
如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k-1图象过点A和点C,抛物线与x轴的另一交点是B,查看答案和解析>>
科目:初中数学 来源: 题型:
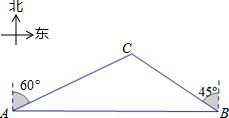 如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,可疑渔船正向西北方向航行,我渔政船立即沿北偏东60°方向航行,在我领海区域的C处截获可疑渔船.我渔政船的航行路程AC为18是海里,问可疑渔船的航行路程BC是多少海里?(结果保留根号)
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,可疑渔船正向西北方向航行,我渔政船立即沿北偏东60°方向航行,在我领海区域的C处截获可疑渔船.我渔政船的航行路程AC为18是海里,问可疑渔船的航行路程BC是多少海里?(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com