
 (1)计算:(-$\frac{1}{2}$)-1+$\sqrt{3}$tan30°-sin245°
(1)计算:(-$\frac{1}{2}$)-1+$\sqrt{3}$tan30°-sin245°分析 (1)利用特殊角的三角函数值、负整数指数幂的意义计算;
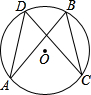
(2)根据圆心角、弧、弦的关系得到$\widehat{AD}$=$\widehat{BC}$,则$\widehat{AB}$=$\widehat{CD}$,所以AB=CD.
解答 (1)解:原式=-2+$\sqrt{3}$×$\frac{\sqrt{3}}{3}$-($\frac{\sqrt{2}}{2}$)2
=-2+1-$\frac{1}{2}$
=-$\frac{3}{2}$;
(2)证明:∵AD=BC,
∴$\widehat{AD}$=$\widehat{BC}$,
∴$\widehat{AD}$+$\widehat{BD}$=$\widehat{BD}$+$\widehat{BC}$,
即$\widehat{AB}$=$\widehat{CD}$,
∴AB=CD.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了实数的运算.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
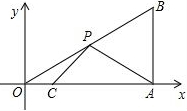 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,点P是斜边DB上的一个动点,则△PAC的周长的最小值为2$\sqrt{7}$+4.
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,点P是斜边DB上的一个动点,则△PAC的周长的最小值为2$\sqrt{7}$+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,⊙O的面积为1,点P为⊙O上一点,令记号【n,m】表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后,半径OP扫过的面积.旋转的规则为:第1次旋转m度;第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度:第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度;第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度…依此类推.例如【2,90】=$\frac{3}{8}$,则【2017,180】=$\frac{{2}^{2017}-1}{{2}^{2017}}$.
如图所示,⊙O的面积为1,点P为⊙O上一点,令记号【n,m】表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后,半径OP扫过的面积.旋转的规则为:第1次旋转m度;第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度:第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度;第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度…依此类推.例如【2,90】=$\frac{3}{8}$,则【2017,180】=$\frac{{2}^{2017}-1}{{2}^{2017}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com