三角形的三个内角度数比为1:2:3.则三个外角的度数比为5:4:3．题目和参考答案——青夏教育精英家教网—

18．三角形的三个内角度数比为1：2：3，则三个外角的度数比为5：4：3．

分析先根据三个内角度数的比设未知数，根据三角形的内角和列一元一次方程求出x的值，再求其对应的三个外角的度数并求比值即可．

解答解：设此三角形三个内角的比为x，2x，3x，
则x+2x+3x=180，
6x=180，
x=30，
∴三个内角分别为30°、60°、90°，
相应的三个外角分别为150°、120°、90°，
则三个外角的度数比为：150°：120°：90°=5：4：3，
故答案为：5：4：3．

点评本题考查了三角形的内角和定理和外角的性质，比较简单，明确三角形的内角和为180°，并熟知三角形的一个内角与其相邻的外角和为180°．

练习册系列答案

暑假星生活黄山书社系列答案

相关习题

科目：初中数学 来源： 题型：填空题

8．用表示大小关系的符号填空：
（1）a²≥0；
（2）-|x|≤0；
（3）x²+1＞0；
（4）x²-2xy+y²≥0．

科目：初中数学 来源： 题型：解答题

9．

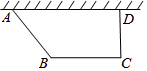如图，要建造一个直角梯形的花圃，要求AD边靠墙，CD⊥AD，AB：CD=5：4，另外三边的和为20米，设AB的长为5x米
（1）求出AD的长；（用含字母x的式子表示）
（2）若该花圃的面积为50平方米，且周长不大于30米，求AB的长．

科目：初中数学 来源： 题型：解答题

6．

（1）计算：（-$\frac{1}{2}$）^-1+$\sqrt{3}$tan30°-sin²45°
（2）已知：如图，AD、BC是⊙O的两条弦，且AD=BC，求证：AB=CD．

科目：初中数学 来源： 题型：选择题

13．

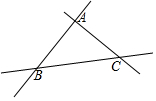如图是三条两两相交的笔直公路，现欲修建一个加油站，使它到三条公路的距离相等，这个加油站应建在（　　）

	A．	△ABC三边的中线的交点上		B．	△ABC三边垂直平分线的交点上
	C．	△ABC三条边高的交点上		D．	△ABC三内角平分线的交点上

科目：初中数学 来源： 题型：填空题

3．已知0≤x≤3，化简$\sqrt{x^2}-\sqrt{{x^2}-6x+9}$=2x-3．

科目：初中数学 来源： 题型：选择题

10．已知x^a+a=3是关于x的一元一次方程，则该方程的解为（　　）

A．

x=1

B．

x=2

C．

x=3