
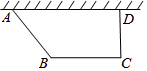
 如图,要建造一个直角梯形的花圃,要求AD边靠墙,CD⊥AD,AB:CD=5:4,另外三边的和为20米,设AB的长为5x米
如图,要建造一个直角梯形的花圃,要求AD边靠墙,CD⊥AD,AB:CD=5:4,另外三边的和为20米,设AB的长为5x米分析 (1)作BE⊥AD于E,就可以得出BE=CD,在Rt△ABE中由勾股定理就可以求出AE,由BC=DE就可以表示出AD而得出结论;
(2)由(1)的结论根据梯形的面积公式求出x的值,建立不等式求出x的取值范围就可以得出结论.
解答 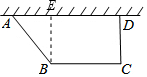 解:(1)作BE⊥AD于E,
解:(1)作BE⊥AD于E,
∴∠AEB=∠DEB=90°.
∵CD⊥AD,
∴∠ADC=90°.
∵BC∥AD,
∴∠EBC=90°,
∴四边形BCDE是矩形,
∴BE=CD,BC=DE.
∵AB:CD=5:4,AB的长为5x米,
∴CD=4x米,
∴BE=4x,
在Rt△ABE中,由勾股定理,得
AE=3x.
∵BC=20-5x-4x=20-9x,
∴DE=20-9x,
∴AD=20-9x+3x=20-6x;
(2)∵AB+BC+CD+DA≤30,
∴5x+20-9x+4x+20-6x≤30,
∴x≥$\frac{5}{3}$,
又∵$\frac{1}{2}$(AD+BC) CD=50,即$\frac{1}{2}$(20-9x+20-6x)•4x=50,
即3x2-8x+5=0,解之得:x1=1,x2=$\frac{5}{3}$,
∵x≥$\frac{5}{3}$,故只取x=$\frac{5}{3}$,
∵AB=5x,
∴AB=$\frac{25}{3}$,
∴AB的长为$\frac{25}{3}$米.
点评 本题考查了勾股定理的运用,梯形的面积公式的运用,梯形的周长公式的运用,一元二次方程的解法的运用,一元一次不等式的运用,解答时根据条件建立方程及不等式是关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:填空题
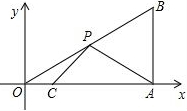 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,点P是斜边DB上的一个动点,则△PAC的周长的最小值为2$\sqrt{7}$+4.
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,点P是斜边DB上的一个动点,则△PAC的周长的最小值为2$\sqrt{7}$+4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com