
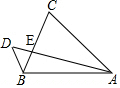
 如图.在△ABC中,AB=AC,D为△ABC外一点,连结AD,交BC于点E,连结DB,若∠C=∠D,AE=8,DE=2.求AC的长.
如图.在△ABC中,AB=AC,D为△ABC外一点,连结AD,交BC于点E,连结DB,若∠C=∠D,AE=8,DE=2.求AC的长. 分析 由AB=AC知∠ABE=∠C,结合∠C=∠D得∠ABE=∠D,利用∠BAE=∠DAB证△ABE∽△ADB得$\frac{AB}{AD}=\frac{AE}{AB}$,从而得出AB=AC=4$\sqrt{5}$.
解答 解:如图,
∵AB=AC,
∴∠ABE=∠C,
∵∠C=∠D,
∴∠ABE=∠D,
又∵∠BAE=∠DAB,
∴△ABE∽△ADB,
∴$\frac{AB}{AD}=\frac{AE}{AB}$,即$\frac{AB}{8+2}$=$\frac{8}{AB}$,
解得:AB=4$\sqrt{5}$,
∴AC=AB=4$\sqrt{5}$.
点评 本题主要考查相似三角形的判定与性质及等腰三角形的性质,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,判定三角形相似的方法有事可单独使用,有时需要综合运用,无论是单独使用还是综合运用,都要具备应有的条件方可.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
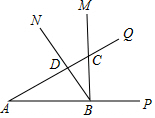 如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 4 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
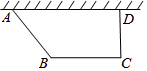 如图,要建造一个直角梯形的花圃,要求AD边靠墙,CD⊥AD,AB:CD=5:4,另外三边的和为20米,设AB的长为5x米
如图,要建造一个直角梯形的花圃,要求AD边靠墙,CD⊥AD,AB:CD=5:4,另外三边的和为20米,设AB的长为5x米查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
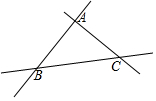 如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )
如图是三条两两相交的笔直公路,现欲修建一个加油站,使它到三条公路的距离相等,这个加油站应建在( )| A. | △ABC三边的中线的交点上 | B. | △ABC三边垂直平分线的交点上 | ||
| C. | △ABC三条边高的交点上 | D. | △ABC三内角平分线的交点上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com