
【题目】如图,正方形![]() 的边长为6个单位长度,点
的边长为6个单位长度,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 从点
从点![]() 出发,以1个单位/秒的速度按
出发,以1个单位/秒的速度按![]() 的方向运动,再次回到
的方向运动,再次回到![]() 点结束运动,设
点结束运动,设![]() 点运动的时间为
点运动的时间为![]() 秒.
秒.

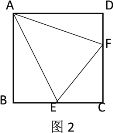

(1)如图1,若![]() 为直角三角形,求
为直角三角形,求![]() 的值;
的值;
(2)如图2,若点![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,点![]() 是对角线
是对角线![]() 的三等分点,且
的三等分点,且![]() ,若
,若![]() ,直接写出满足条件的
,直接写出满足条件的![]() 点的个数,并注明这些
点的个数,并注明这些![]() 点分别在正方形的哪条边上.
点分别在正方形的哪条边上.
【答案】(1)4.5或12或21;(2)135°;(3)有两个,分别在![]() 和
和![]() 上
上
【解析】
(1)分当点F在CD上、AD上以及和点B重合时三种情况分别求出相应的t值;
(2)根据题意求出DF和CF,EF,延长![]() 至点
至点![]() ,证明
,证明![]() ,得到
,得到![]() ,
,![]() ,再证明
,再证明![]() ,得到对应角相等,最后根据
,得到对应角相等,最后根据![]() 可得结果;
可得结果;
(3)分点F在正方形各边上的情况,分别求出![]() 的最值,即可得出结果.
的最值,即可得出结果.
解:(1)①当点![]() 在
在![]() 上,
上,![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() ,
,
解之:![]() ,
,
②当点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,
③当点![]() 与
与![]() 点重合,
点重合,![]() ,
,![]() ,
,
(2)解:∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
延长![]() 至点
至点![]() ,使
,使![]() ,
,
则![]() ,
,
在![]() 与
与![]() 中,
中,
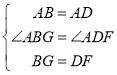 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
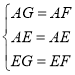 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
又∵在![]() 中,
中,![]() ,
,
∴![]() ;
;
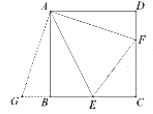
(3)满足条件的![]() 点有两个,分别在
点有两个,分别在![]() 边和
边和![]() 上.
上.
理由是:当点F在AB上时,如图,
E′为点E关于AB的对称点,GH⊥BC于H,
∵GH∥CD,
∴![]() ,
,
可得GH=BH=4,
∴![]() 的最小值为E′G=
的最小值为E′G=![]() >8,
>8,
即AB上没有符合要求的F;
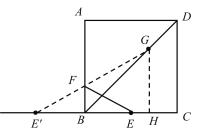
当点F在AD上时,如图,
E′为点E关于AD的对称点,
同理可得:KG=![]() AB=2,HG=6+2=8<E′G,
AB=2,HG=6+2=8<E′G,
∴此时![]() 的最小值为E′G的长,大于8,
的最小值为E′G的长,大于8,
∴AD上不存在符合要求的F;

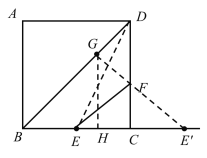
当点F在CD上时,如图,
E′为点E关于CD的对称点,GH⊥BC于H,
同理可得:GH=BH=4,HC=2,
∴HE′=5,
此时![]() 的最小值为E′G=
的最小值为E′G=![]() <8,
<8,
当点F在点D处时,![]() =ED+GD=
=ED+GD=![]() =
=![]() ,
,
∴CD上存在符合要求的点F;
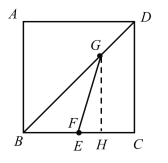
当点F在BC上时,GH⊥BC于H,
若点F与点E重合,
同理可知GH=4=BH,EH=BH-BE=1,
则![]() =GE=
=GE=![]() <8,
<8,
若点F与点B重合,
同理可知BG=![]() ,BE=3,
,BE=3,
则![]() =BE+BG=
=BE+BG=![]() =8,
=8,
故BC上存在符合要求的点F;
综上:满足条件的![]() 点有两个,分别在
点有两个,分别在![]() 和
和![]() 上.
上.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.
(1) 求每辆小客车和每辆大客车的乘客座位数;
(2) 由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场准备购进甲.乙两种商品,若购进甲商品80个,乙商品40个,需要800元;若购进甲商品50个,乙商品30个,需要550元.
(1)求商场购进甲.乙两种商品每个需要多少元?
(2)商场准备1000元全部用来购进甲.乙两种商品,计划销售每个甲种商品可获利润4元,销售每个乙种商品可获利润5元,销售这两种玩具的总利润不低于600元,那么商场最多购进乙种商品多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
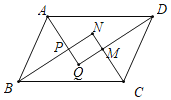
【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“读书破万卷,下笔如有神”,这是古人关于读书的成功经验.开展课外阅读可以引起学生浓厚的学习兴趣和探求知识的强烈欲望,丰富知识,开阔视野,也有利于学习和巩固老师在课堂上所教的基础知识,使学生学得有趣,学得扎实,学得活泼,是启发智慧和锻炼才能的一条重要途径.为了创设全新的校园文化氛围,进一步组织学生开展课外阅读,让学生在丰富多彩的书海中,扩大知识源,亲近母语,提高文学素养.某校准备开展“与经典为友、与名著为伴”的阅读活动,活动前对本校学生进行了“你最喜欢的图书类型(只写一项)”的随机抽样调查,相关数据统计如下:

请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整,并求出扇形统计图中小说所对应的圆心角度数.
(3)已知该校共有学生800人,利用样本数据估计全校学生中最喜欢小说人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() ,
,![]() ,且以
,且以![]() 为顶点的四边形为菱形.
为顶点的四边形为菱形.

(1)直接写出![]() 点的坐标;
点的坐标;
(2)请用无刻度直尺作直线![]() ,使直线
,使直线![]() 经过点
经过点![]() 且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);
且平分菱形的面积,保留作图痕迹(若无法打印答题卡,不便于规范作图,请用几何语言直接描述具体的作图过程代替作图);
(3)已知点![]() 是
是![]() 边上一点,若线段
边上一点,若线段![]() 将菱形
将菱形![]() 的面积分为
的面积分为![]() 两部分,直接写出点
两部分,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明租用共享单车从家出发,匀速骑行到相距2400米的邮局办事.小明出发的同时,他的爸爸以每分钟100米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
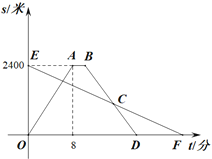
(1)求s1与t之间的函数表达式;
(2)小明从家出发,经过_______分在返回途中追上爸爸.
查看答案和解析>>
科目:初中数学 来源: 题型:
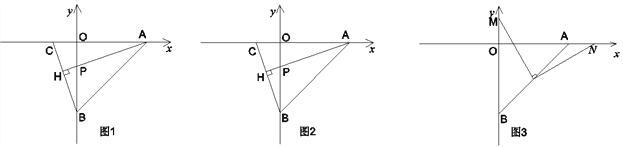
【题目】如图1,直线AB交x轴于点A(4 ,0),交y轴于点B(0 ,4),
(1)如图,若C的坐标为(-1, ,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;
(2)在(1)的条件下,如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连结MD,过点D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,式子![]() 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com