
分析 (1)关键描述语:企业购买设备的资金不高于105万元,列出不等式进行求解.
(2)关键描述语:企业每月产生的污水量为2040吨,即每月A和B型两种设备的污水处理量应大于等于2040吨,且为了节约资金,所需的费用应为最少.
解答 解:(1)设购买污水处理设备A型x台,则B型(10-x)台,根据题意得
$\left\{\begin{array}{l}{x≥0}\\{12x+10(10-x)≤105}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x≥0}\\{2x≤5}\end{array}\right.$,即0≤x≤$\frac{5}{2}$,
∵x为整数,
∴x可取0,1,2,
当x=0时,10-x=10,
当x=1,时10-x=9,
当x=2,时10-x=8,
即有三种购买方案:
方案一:不买A型,买B型10台;
方案二,买A型1台,B型9台;
方案三,买A型2台,B型8台.
(2)由240x+200(10-x)≥2040
解得x≥1,
由(1)得1≤x≤2.5
故x=1或x=2
当x=1时,购买资金12×1+10×9=102(万元)
当x=2时,购买资金12×2+10×8=104(万元)
∵104>102
∴为了节约资金应购买A型1台,B型9台,即方案二.
点评 本题主要考查了不等式组在现实生活中的应用,根据已知A,B型号的设备其价格得出正确等量关系是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{19}{100}$ | C. | $\frac{1}{20}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 46 | B. | 45 | C. | 44 | D. | 43 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
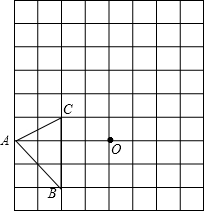 如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:
如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
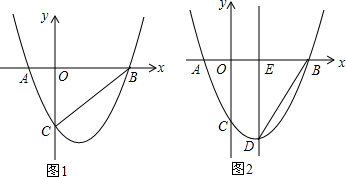
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com