
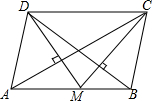
 点M在平行四边形ABCD的边AB上,满足AM:MB=4:3,且DM和CM分别垂直于AC和BD.若BC=5cm,请问?ABCD的面积是多少cm2?
点M在平行四边形ABCD的边AB上,满足AM:MB=4:3,且DM和CM分别垂直于AC和BD.若BC=5cm,请问?ABCD的面积是多少cm2? 分析 由平行四边形的性质得出△ODN≌△OBM,进而得出OM=ON,DN=BM,CN=AM,由DM⊥AC,CM⊥BD,可得点O是△CDM的垂心,由AM:MB=4:3得$\frac{BF}{DF}$=$\frac{BM}{CD}$=$\frac{3}{7}$,由△DON∽△MOF,得出OD•OF=OM•ON,从而得出BD=$\sqrt{10}$OM,由勾股定理可昨CD=$\frac{7}{3}$DN=$\frac{7}{3}$$\sqrt{O{D}^{2}-O{N}^{2}}$,再利用△DON∽△DCF,可求出CF的值,在RT△BCF中,利用勾股定理可得OM2=6,运用S平行四边形ABCD=CD•MN即可求解.
解答 解:连接MO并延长交CD于点N,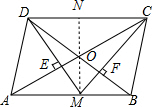
∵四边形ABCD是平行四边形,点O为对角线的交点
∴DO=BO,∠DON=∠BOM,∠NDO=∠MBO,
在△ODN和△OBM中,
$\left\{\begin{array}{l}{∠NDO=∠MBO}\\{DO=BO}\\{∠DON=∠BOM}\end{array}\right.$,
∴△ODN≌△OBM(ASA),
∴OM=ON,DN=BM,
∴CN=AM,
∵DM⊥AC,CM⊥BD,
∴点O是△CDM的垂心,
∴MN⊥CD,
由AB∥CD,AM:MB=4:3得:$\frac{BF}{DF}$=$\frac{BM}{CD}$=$\frac{3}{7}$,
∴BF=$\frac{3}{10}$BD,OD=$\frac{1}{2}$BD,OF=$\frac{1}{5}$BD,
∵∠DNO=∠MFO=90°,∠DON=∠MOF,
∴△DON∽△MOF,
∴OD•OF=OM•ON,
∴$\frac{1}{2}$BD•$\frac{1}{5}$BD=OM2,得BD=$\sqrt{10}$OM,
∴OD=$\frac{\sqrt{10}OM}{2}$,BF=$\frac{3\sqrt{10}}{10}$OM,DF=$\frac{7\sqrt{10}}{10}$OM,ON=OM,
而CD=$\frac{7}{3}$DN=$\frac{7}{3}$$\sqrt{O{D}^{2}-O{N}^{2}}$=$\frac{7}{3}$×$\frac{\sqrt{6}}{2}$OM=$\frac{7\sqrt{6}}{6}$OM,
由△DON∽△DCF,得$\frac{CF}{ON}$=$\frac{CD}{OD}$,
∴CF=$\frac{7\sqrt{15}}{15}$,
在RT△BCF中,BF2+CF2=BC2=25得OM2=6,
∴S平行四边形ABCD=CD•MN=$\frac{7\sqrt{6}}{6}$OM•2OM=$\frac{7\sqrt{6}}{3}$OM2=14$\sqrt{6}$(平方厘米).
答:?ABCD的面积是14$\sqrt{6}$cm2.
点评 本题主要考查了面积及等积变换,涉及平行四边形的性质,全等三角形的判定及性质,相似三角形的判定及性质,勾股定理等知识,解题的关键是正确作出辅助线,利用相似三角形求出CF的值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
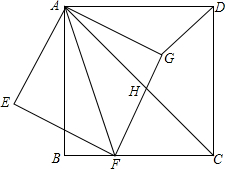 如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com