
【题目】如图所示,M,N分别是OA,OB边上的点,点P在射线OC上,则下列条件中不能说明OC平分∠AOB的是( )
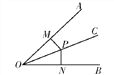
A. PM⊥OA,PN⊥OB,PM=PN B. PM=PN,OM=ON
C. PM⊥OA,PN⊥OB,OM=ON D. PM=PN,∠PMO=∠PNO
【答案】D
【解析】A中,PM⊥OA,PN⊥OB,PM=PN,根据角平分线的判定:到角两边距离相等的点在角的平分线上,可知OC平分∠AOB,选项A正确;
B中,PM=PN,OM=ON,又因为OP=OP,得△OPM≌△OPN,所以∠AOC=∠BOC,所以OC平分∠AOB,选项B正确;
C中,PM⊥OA,PN⊥OB,在Rt△OPM与Rt△OPN中,OM=ON,OP=OP,所以Rt△OPM≌Rt△OPN,所以∠AOC=∠BOC,所以OC平分∠AOB,选项C正确;
D中,在△OPM与△OPN中,已知PM=PN, OP=OP,∠PMO=∠PNO,无法判断△OPM≌△OPN,故无法判断OC平分∠AOB,选项D错误.
故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
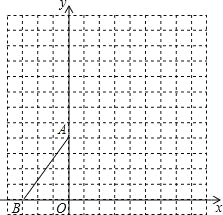
【题目】如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(﹣3,0),按要求解答下列问题.
(1)在图中,先将△AOB向上平移6个单位,再向右平移3个单位,画出平移后的△A1O1B1;(其中点A,O,B的对应点为A1,O1,B1)
(2)在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1,B1的对应点为A2,B2)
(3)直接写出点A2,B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥整个大桥造价超过720亿元人民币,720亿用科学记数法可表示为( )元.
A. 7.2×1010B. 0.72×1011C. 7.2×1011D. 7.2×109
查看答案和解析>>
科目:初中数学 来源: 题型:
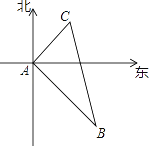
【题目】如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,某省2015年的贫困人口约382万,截止2017年底,全省贫困人口约190万,设这两年全省贫困人口的年平均下降率为x,则下列方程正确的是( )
A. 382(1﹣2x)=190B. 382x2=190
C. 382(1﹣x)2=190D. 382(1﹣x)+382(1﹣x)2=190
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社带一旅游团来宜春明月山游玩,晚上入住温汤某酒店,现需要订9个房间,酒店房间分为两种:A种房间200元/间,B种房间160/间,在费用不超过1700元的情况下,要求A种房间的数量不少于B种房间数量的一半.若设订A种房间x间,请你解答下列问题:
(1)共有几种符合题意的订房方案?写出解答过程.
(2)根据计算判断:哪种订房方案更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!
(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5![]() ,FC=2时,求EF的长度;
,FC=2时,求EF的长度;
(2)如图2,若点D为等边三角形ABC边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;
(3)如图3,若点D为等边三角形ABC边BC的中点,点E、F分别在AB、AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com