
����Ŀ��ij����ÿ���ܳ��ۼס��������⼯װ�乲21�䣬�Ҽ�װ��3������������Ҽ�װ��4�����������ͬ��
��1����ס����������༯װ��ÿ��ֱ��ܳ��۶����䣿
��2�����������༯װ��Ľ���Ϊÿ��200Ԫ���������༯װ��Ľ���Ϊÿ��180Ԫ���ֳ��д��㹺��ס����������༯װ�乲100�䣬����ͷ�ʽ�18080Ԫ����ó����м��ֹ�����
��3�����������༯װ����ۼ�Ϊÿ��260Ԫ���������༯װ����ۼ�Ϊÿ��230Ԫ���ڣ�2��������£����ַ���������ࣿ
���𰸡���1���ס����������༯װ��ÿ��ֱ��ܳ���12���9�䣻
��2������һ������������༯װ��1�䣬�����������༯װ��99�䣻
������������������༯װ��2�䣬�����������༯װ��98�䣻
������������������༯װ��3�䣬�����������༯װ��97�䣻
��3��������������࣮
��������
�����������1����ס����������༯װ��ÿ��ֱ��ܳ���x���y�䣬����ÿ���ܳ��ۼס��������⼯װ�乲21��ͼ�װ��3������������Ҽ�װ��4�����������ͬ���г������飬��⼴�ɣ�
��2����������༯װ�乺��a��a��0���䣬�������༯װ�乺��100��a���䣬���ݼס����������༯װ�乲100�䣬����ͷ�ʽ�18080Ԫ���г�����ʽ������⼴�ɣ�
��3�����ݣ�2���ó��ķ������ֱ���������һ���������ͷ������Ļ���������ٽ��бȽϼ��ɵó��𰸣�
�����������1����ס����������༯װ��ÿ��ֱ��ܳ���x���y�䣬��������ã�
![]() ��
��
��ã�![]() ��
��
�𣺼ס����������༯װ��ÿ��ֱ��ܳ���12���9�䣻
��2����������༯װ�乺��a��a��0���䣬�������༯װ�乺��100��a���䣬��������ã�
200a+180��100��a����18080��
��ã�a��4��
��a����������
��a=1��2��3��
���ó��������ֹ�����
����һ������������༯װ��1�䣬�����������༯װ��99�䣻
������������������༯װ��2�䣬�����������༯װ��98�䣻
������������������༯װ��3�䣬�����������༯װ��97�䣻
��3��������һ�����ǣ���260��200����1+��230��180����99=5010��Ԫ����
�����������ǣ���260��200����2+��230��180����98=5020��Ԫ����
�����������ǣ���260��200����1+��230��180����99=5030��Ԫ����
��������������࣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�������ax2+bx+c�Ķ�������ʽ������һ���֣������ȫƽ��ʽ�ķ��������䷽�����䷽���Ļ�����ʽ����ȫƽ����ʽ����д����a2��2ab+b2=��a��b��2 �� �����������ʽx2��2x+9���䷽�������£�x2��2x+9=x2��2x+1��1+9=��x��1��2+8��
������Ķ����Ͻ���������⣺
��1��������������ӣ��������������������ʽ�ֱ��䷽��
��x2��4x+1=��
��3x2+6x��9=3��x2+2x����9=��
��2����֪x2+y2��6x+10y+34=0����3x��2y��ֵ��
��3����֪a2+b2+c2+ab��3b+2c+4=0����a+b+c��ֵ��#AE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����Ϊ22cm�Ŀ��ӣ����ڵ���ֱ��Ϊ5cm����Ϊ12cm��Բ����ˮ���У������¶�ڱ�������ij���Ϊhcm����h��ȡֵ��Χ�� �� ����

A. 9cm��h��10cm B. 10cm��h��11cm C. 12cm��h��13cm D. 8cm��h��9cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪BEƽ�֡�ABC����1=��2����֤����AED=��C�����������������̣� ֤������BEƽ�֡�ABC�����1=��3�� ����
�֡ߡ�1=��2����֪������=�� ������������
��������
���AED=��C ������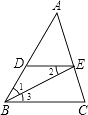
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��������������ͼ���㣨��1��3��������������������ı���ʽ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���һ������P0��1��0���������˶�1����λ������P1��1��1����Ȼ�������˶�2����λ��P2�����������˶�3����λ��P3�����������˶�4����λ��P4�����������˶�5����λ��P5��������˼����˶���ȥ����Pn��xn �� yn����n=1��2��3������x1+x2+��+x99+x100=�� �� 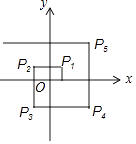
A.0
B.��49
C.50
D.��50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ϸ����ֱ����0.00000085�ף������ÿ�ѧ��������ʾΪ ( )
A. 8.5��10-8B. 8.5��10-7C. 0.85��10-7D. 85��10-8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,M,N�ֱ���OA,OB���ϵĵ�,��P������OC��,�����������в���˵��OCƽ�֡�AOB����( )
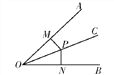
A. PM��OA,PN��OB,PM=PN B. PM=PN,OM=ON
C. PM��OA,PN��OB,OM=ON D. PM=PN,��PMO=��PNO
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com