
【题目】如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程. 证明:∵BE平分∠ABC,∴∠1=∠3. ()
又∵∠1=∠2(已知),∴=( 等量代换),
∴∥()
∴∠AED=∠C ().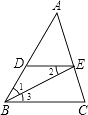
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
【题目】据统计,2018年3月,三峡大坝共接待旅游人数约4 700 000人次,4 700 000这个数用科学计数法表示为( )
A. 47×106B. 4.7×105C. 4.7×107D. 4.7×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材中,在计算如图1所示的正方形ABCD的面积时,分别从两个不同的角度进行了操作: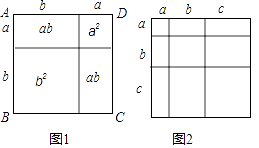
(i)把它看成是一个大正方形,则它的面积为(a+b)2;
(ii)把它看成是2个小长方形和2个小正方形组成的,则它的面积为a2+2ab+b2;因此,可得到等式:(a+b)2=a2+2ab+b2 .
(1)类比教材中的方法,由图2中的大正方形可得等式: .
(2)试在图2右边空白处画出面积为2a2+3ab+b2的长方形的示意图(标注好a,b) ,由图形可知,多项式2a2+3ab+b2可分解因式为: .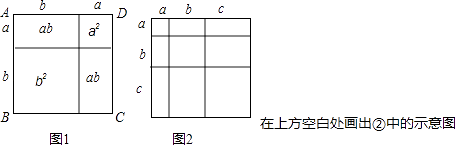
(3)若将代数式(a1+a2+a3+…+a20)2展开后合并同类项,得到多项式N,则多项式N的项数一共有项.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4) 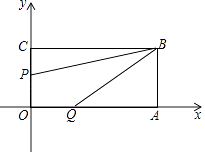
(1)填空:点A的坐标为 , 点C的坐标为 , 点P的坐标为 . (用含t的代数式表示)
(2)当t为何值时,P、Q两点与原点距离相等?
(3)在点P、Q移动过程中,四边形OPBQ的面积是否变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
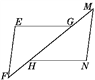
【题目】如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出所有相等的线段与相等的角;
(2)若EF=2.1 cm,FH=1.1 cm,HM=3.3 cm,求MN和HG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥整个大桥造价超过720亿元人民币,720亿用科学记数法可表示为( )元.
A. 7.2×1010B. 0.72×1011C. 7.2×1011D. 7.2×109
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com