
【题目】如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4) 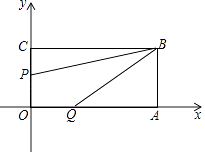
(1)填空:点A的坐标为 , 点C的坐标为 , 点P的坐标为 . (用含t的代数式表示)
(2)当t为何值时,P、Q两点与原点距离相等?
(3)在点P、Q移动过程中,四边形OPBQ的面积是否变化?说明理由.
【答案】
(1)(8,0);(0,4);(0,4﹣t)
(2)解:依题意可知:OP=4﹣t,OQ=2t,若OP=OQ,则有:4﹣t=2t
解之得,t= ![]() .
.
∴当t= ![]() 时,点P和点Q到原点的距离相等
时,点P和点Q到原点的距离相等
(3)解:四边形OPBQ的面积不变.理由如下:
∵S四边形OPBQ=S矩形OABC﹣S△PCB﹣S△ABQ
=32﹣ ![]() 8t﹣
8t﹣ ![]() 4(8﹣2t)
4(8﹣2t)
=32﹣4t﹣16+4t
=16.
∴四边形OPBQ的面积不变.
【解析】解:(1)由题意可知点A的坐标为 (8,0),点C的坐标为 (0,4),点P的坐标为 (0,4﹣t).(用含t的代数式表示), 故答案分别为(8,0),(0,4),(0,4﹣t).
(1)根据点坐标的定义即可解决问题;(2)由题意OP=OQ,则有:4﹣t=2t,解方程即可;(3)四边形OPBQ的面积.通过S四边形OPBQ=S矩形OABC﹣S△PCB﹣S△ABQ计算证明即可;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】体育课上,某班两名同学分别进行了5次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较两名同学成绩的( )
A.平均数 B.方差 C.众数 D.中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲种蔬菜比乙种蔬菜单价少5角,张阿姨买了2斤甲蔬菜和3斤乙蔬菜,一共花了20元,如果设甲种蔬菜的单价为x元/斤,那么下列方程正确的是( )
A. 2x+3(x+5)=20 B. 2x+3(x+0.5)=20 C. 2x+3(x-0.5)=20 D. 2x+3(x-5)=20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题4分)把下列各数分别填入相应的集合内:
-2.5,0,-0.5252252225…(每两个5之间依次增加1个2),100%,-(-2),![]() ,
,![]()
(1)正数集合:{ …};
(2)负分数集合:{ …};
(3)整数集合:{ …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程. 证明:∵BE平分∠ABC,∴∠1=∠3. ()
又∵∠1=∠2(已知),∴=( 等量代换),
∴∥()
∴∠AED=∠C ().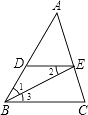
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
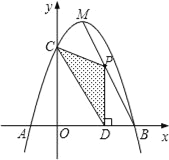
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,设一动点自P0(1,0)处向上运动1个单位长度至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn , yn),n=1,2,3,…则x1+x2+…+x99+x100=( ) 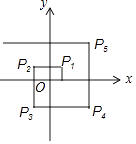
A.0
B.﹣49
C.50
D.﹣50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平移、旋转和轴对称这些图形变换下,它们共同具有的特征是( )
A. 图形的形状、大小没有改变,对应线段平行且相等
B. 图形的形状、大小没有改变,对应线段垂直,对应角相等
C. 图形的形状、大小都发生了改变,对应线段相等,对应角相等
D. 图形的形状、大小没有改变,对应线段相等,对应角相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com