练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】甲种蔬菜比乙种蔬菜单价少5角,张阿姨买了2斤甲蔬菜和3斤乙蔬菜,一共花了20元,如果设甲种蔬菜的单价为x元/斤,那么下列方程正确的是(　　)

    A. 2x+3(x+5)=20 B. 2x+3(x+0.5)=20 C. 2x+3(x-0.5)=20 D. 2x+3(x-5)=20

    【答案】B

    【解析】

    设甲种蔬菜的单价为x元/斤，则乙种蔬菜的单价为（x+0.5）元/斤，根据题意可得等量关系：2斤甲蔬菜的花费+3斤乙蔬菜的花费=20元，根据等量关系列出方程即可．

    设甲种蔬菜的单价为x元/斤，由题意得：

    2x+3(x+0.5)=20，

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在三角形纸片ABC中，∠B=∠C=35°，过边BC上的一点，沿与BC垂直的方向将它剪开，分成三角形和四边形两部分，则在四边形中，最大的内角的度数为（ ）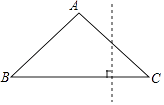
    A.110°
    B.115°
    C.120°
    D.125°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知xa=3，xb=5，则x2a+b= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点P( 2，－3 )关于x轴的对称点是(　 　)

    A. (－2， 3 ) B. (2，3) C. (－2，－3 ) D. (2，－3 )

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】长方形的周长为12cm，长是宽的2倍，则长为cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的边长为24厘米，∠A=60°，点P从点A出发沿线路AB→BD作匀速运动，点Q从点D同时出发沿线路DC→CB→BA作匀速运动．

    （1）求BD的长；

    （2）已知点P、Q运动的速度分别为4厘米/秒，5厘米/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请你确定△AMN是哪一类三角形，并说明理由；

    （3）设（2）中的点P、Q分别从M、N同时沿原路返回，点P的速度不变，点Q的速度改变为a厘米/秒，经过3秒后，P、Q分别到达E、F两点，若△BEF与（2）中的△AMN相似，试求a的值．

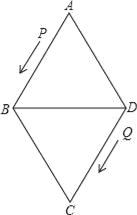
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】教材中，在计算如图1所示的正方形ABCD的面积时，分别从两个不同的角度进行了操作：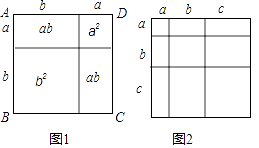

    （i）把它看成是一个大正方形，则它的面积为（a+b）2；
    （ii）把它看成是2个小长方形和2个小正方形组成的，则它的面积为a2+2ab+b2；因此，可得到等式：（a+b）2=a2+2ab+b2 ．
    （1）类比教材中的方法，由图2中的大正方形可得等式： ．
    （2）试在图2右边空白处画出面积为2a2+3ab+b2的长方形的示意图（标注好a，b） ，由图形可知，多项式2a2+3ab+b2可分解因式为： ．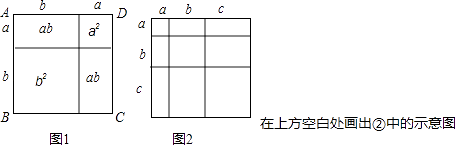

    （3）若将代数式（a1+a2+a3+…+a20）2展开后合并同类项，得到多项式N，则多项式N的项数一共有项．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图长方形OABC的位置如图所示，点B的坐标为（8，4），点P从点C出发向点O移动，速度为每秒1个单位；点Q同时从点O出发向点A移动，速度为每秒2个单位，设运动时间为t（0≤t≤4）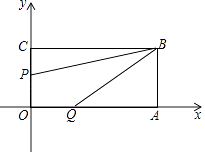
    （1）填空：点A的坐标为 ， 点C的坐标为 ， 点P的坐标为 ． （用含t的代数式表示）
    （2）当t为何值时，P、Q两点与原点距离相等？
    （3）在点P、Q移动过程中，四边形OPBQ的面积是否变化？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB，CD相交于点O，OD平分∠EOB，OF平分∠AOE，GH⊥CD，垂足为H，求证：GH∥FO．

    查看答案和解析>>

    同步练习册答案