练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列命题中，是真命题的是（ ）

    A. 任何数都有平方根 B. 只有正数才有平方根

    C. 负数没有立方根 D. 存在算术平方根等于本身的数

    【答案】D

    【解析】

    根据平方根的定义，结合正数有两个平方根；0的平方根是0；负数没有平方根逐一进行判定即可．

    A、因负数没有平方根，故任何数都有平方根错误；

    B、因0的平方根是0，故只有正数才有平方根错误；

    C、负数有立方根，故负数没有立方根错误；

    D、存在算术平方根等于本身的数，如0的算术平方根是0，故选项D正确．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数 的图象相交于点（2，a）．

    （1）求a的值．
    （2）求一次函数y=kx+b的表达式．
    （3）在同一坐标系中，画出这两个函数的图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若等腰三角形一腰上的高与底边的夹角为n°，则这个等腰三角形顶角等于________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】德国《时代》周报网站列举了数据来评价中国改革开放40年的成就，在2017年我国申报了8330项国际专利，目前在年度国际专利申请量排名中位居第五，8330用科学记数法表示为（　　）

    A. 0.833×104B. 83.3×103C. 8.33×103D. 8.33×104

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．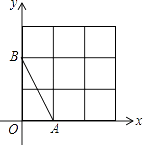

    （1）在网格的格点中，找一点C，使△ABC是直角三角形，且三边长均为无理数（只画出一个，并涂上阴影）；
    （2）若点P在图中所给网格中的格点上，△APB是等腰三角形，满足条件的点P共有个；
    （3）若将线段AB绕点A顺时针旋转90°，写出旋转后点B的坐标 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】地球上七大洲的总面积约为149 480 000km2，精确到1千万km2的结果是_____km2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=﹣x﹣4与抛物线y=ax2+bx+c相交于A，B两点，其中A，B两点的横坐标分别为﹣1和﹣4，且抛物线过原点．

    （1）求抛物线的解析式；

    （2）在坐标轴上是否存在点C，使△ABC为等腰三角形？若存在，求出点C的坐标，若不存在，请说明理由；

    （3）若点P是线段AB上不与A，B重合的动点，过点P作PE∥OA，与抛物线第三象限的部分交于一点E，过点E作EG⊥x轴于点G，交AB于点F，若S△BGF=3S△EFP，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在正方形ABCD中，E，F，G，H分别为边AB，BC，CD，DA上的点，HA=EB=FC=GD，连接EG，FH，交点为O．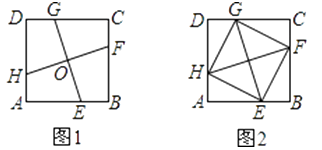

    （1）如图2，连接EF，FG，GH，HE，试判断四边形EFGH的形状，并证明你的结论；
    （2）将正方形ABCD沿线段EG，HF剪开，再把得到的四个四边形按图3的方式拼接成一个四边形．若正方形ABCD的边长为3cm，HA=EB=FC=GD=1cm，则图3中阴影部分的面积为cm2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

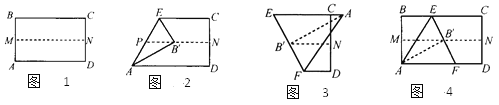
    【题目】取一张矩形纸片进行折叠，具体操作过程如下：第一步：先把矩形ABCD对折，折痕为MN，如图1；第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B'，得Rt△AB'E，如图2；第三步：沿EB'线折叠得折痕EF，使A点落在EC的延长线上，如图3．　　

    利用展开图4探究：

    （1）△AEF是什么三角形?证明你的结论；

    （2）对于任一矩形，按照上述方法是否都能折出这种三角形?请说明理由．

    查看答案和解析>>

    同步练习册答案