
分析 先根据分式混合运算的法则把原式进行化简,再代入原式进行计算即可.
解答 解:(x-$\frac{x}{x+1}$)•$\frac{x+1}{{x}^{2}+4x+4}$÷$\frac{{x}^{2}-2x}{{x}^{2}-4}$
=$\frac{{x}^{2}+x-x}{x+1}•\frac{x+1}{(x+2)^{2}}÷\frac{x(x-2)}{(x-2)(x+2)}$
=$\frac{{x}^{2}}{x+1}•\frac{x+1}{(x+2)^{2}}•\frac{(x-2)(x+2)}{x(x-2)}$
=$\frac{x}{x+2}$,
把x=$\frac{1}{2}$代入$\frac{x}{x+2}=\frac{\frac{1}{2}}{\frac{1}{2}+2}=\frac{1}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
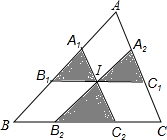 如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )
如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )| A. | 12 | B. | 15 | C. | 18 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com