Question

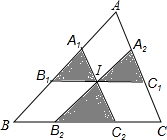
11．如图，△ABC的内切⊙I的半径为4cm，线段B₁C₁，A₁C₂、A₂B₂都经过内心I，并且分别与△ABC的边平行，己知IA₁+IB₂+IC₁=5，△ABC的面积为32m²，则图中阴影部分的面积为（　　）

• A． 12
• B． 15
• C． 18
• D． 20

Answer 1

分析 设△ABC的三边长分别为a、b、c，由内心的性质和已知条件得出a+b+c=16，设IA₁=x，IB₂=y，IC₁=z，证出B₁B=IB₂=C₁C=y，IA₁=AA₂=BB₂=x，IC₁=A₁A=C₂C=z，设A₁B₁=m，B₂C₂=n，A₂C₁=p，求出m+n+p=（a+b+c）-2（x+y+z）=6，图中阴影部分的面积=△IA₁B₁的面积+△IB₂C₂的面积+△IA₂C₁的面积，即可得出结果．

解答 解：设△ABC的三边长分别为a、b、c，
∵I是△ABC的内心，内切圆半径为4cm，
∴△ABC的面积=$\frac{1}{2}$（a+b+c）×4=32，
∴a+b+c=16，
设IA₁=x，IB₂=y，IC₁=z，
∵A₂B₂∥AB，A₁C₂∥AC，B₁C₁∥BC，
∴B₁B=IB₂=C₁C=y，
IA₁=AA₂=BB₂=x，IC₁=A₁A=C₂C=z，
设A₁B₁=m，B₂C₂=n，A₂C₁=p，
∴m=a-（z+y），n=b-（x+z），p=c-（x+y），
∴m+n+p=（a+b+c）-2（x+y+z）=16-2×5=6，
∴图中阴影部分的面积=△IA₁B₁的面积+△IB₂C₂的面积+△IA₂C₁的面积=$\frac{1}{2}$m×4+$\frac{1}{2}$n×4+$\frac{1}{2}$p×4=$\frac{1}{2}$（m+n+p）×4=$\frac{1}{2}$×6×4=12．
故选：A．

点评 本题考查了三角形的内切圆与内心、平行四边形的判定与性质、三角形面积的计算方法等知识；本题综合性强，有一定难度，求出m+n+p是解决问题的关键．