
分析 根据题意画出图形,先求出∠AOB的度数,证明△AOB是等边三角形,得出AB=OA,再根据直角三角形的性质求出OA的长,再根据S六边形=6S△AOB即可得出结论.
解答 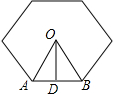 解:如图所示,
解:如图所示,
∵图中是正六边形,
∴∠AOB═60°.
∵OA=OB,
∴△OAB是等边三角形.
∴OA=OAB=AB,
∵OD⊥AB,OD=2$\sqrt{3}$,
∴OA=$\frac{OD}{sin60°}$=4.
∴AB=4,
∴S△AOB=$\frac{1}{2}$AB×OD=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$,
∴正六边形的面积=6S△AOB=6×4$\sqrt{3}$=24$\sqrt{3}$.
故答案为:24$\sqrt{3}$.
点评 本题考查的是正多边形和圆,熟知正六边形的性质,求出△AOB的面积是解答此题的关键.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:选择题
 如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )
如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )| A. | $\frac{BC}{AC}$=$\frac{\sqrt{5}-1}{2}$ | B. | AC+BC=$\frac{\sqrt{5}-1}{2}$AB | C. | $\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$ | D. | AC2=AB•BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
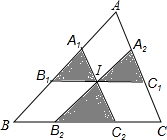 如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )
如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )| A. | 12 | B. | 15 | C. | 18 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-6,3) | B. | (6,3) | C. | (-6,75) | D. | (6,75) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 购买1张彩票,中奖 | |
| B. | 同旁内角互补 | |
| C. | 打开电视,正在播放《动物世界》 | |
| D. | 3个人分成两组,一定有2个人分在一组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com